Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 146
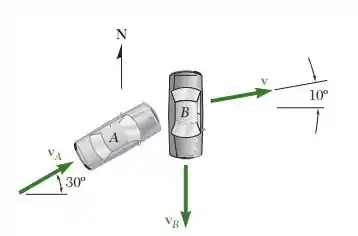
Em um cruzamento, o carro B ia para o sul e o carro A viajava 30° para nordeste, quando se envolveram em uma colisão. Pela investigação, soube-se que, após a batida, os dois carros se engataram e derraparam em um ângulo de 10° para nordeste. Cada motorista declarou que dirigia à velocidade limite de 50 km/h e que tentou reduzir a velocidade, mas que não pôde evitar a batida porque o outro motorista vinha muito mais rápido. Sabendo que as massas dos carros A e B eram de 1.500 kg e 1.200 kg, respectivamente, determine (a) que carro andava mais rápido, (b) a velocidade do carro mais rápido se o carro mais lento se deslocava na velocidade limite.
Passo 1
Essa é uma questão boa para saber quem está mentindo em um acidente de trânsito como esse. Vamos lá. Primeiro temos que saber qual dos dois carros estava mais rápido. Para isso, vamos usar a conservação de quantidade de movimento linear com a finalidade de descobrir isso. Observando o diagrama de corpo livre:
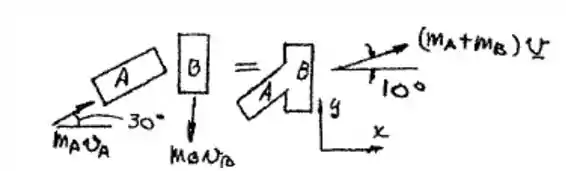
Como os carros se movimentam em direções diferentes, vamos ter uma componente em cada direção:
Passo 2
Para obter uma relação entre as velocidades de A e B, vamos dividir a equação 2 pela a equação 1:
Então temos que o carro A estava mais rápido.
Passo 3
Como o carro A estava mais rápido, o carro B estava se movimentando a 50 km/h. Assim, a velocidade do carro A era:
Resposta
- O carro A estava mais rápido
- 115,2 km/h