Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 13.Problemas - Ex. 149

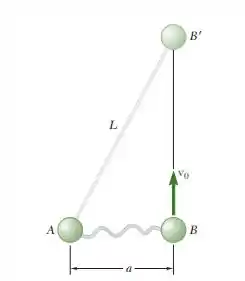
Duas esferas idênticas A e B, cada uma com massa m, estão conectadas por uma corda inextensível e não elástica de comprimento L, e em repouso a uma distância a uma da outra sobre uma superfície horizontal sem atrito. A esfera B recebe uma velocidade v 0 em uma direção perpendicular à linha AB e se move sem atrito até atingir a posição B, quando a corda fica tensionada. Determine (a) a intensidade da velocidade de cada esfera imediatamente depois que a corda fica tensionada, (b) a energia perdida quando a corda fica tensionada.

Passo 1

Esta é uma questão que a gente usar a conservação da quantidade de movimento. A corda, no momento inicial, não está esticada quando B começa seu movimento. Em um segundo momento, a corda fica tensionada e não há atrito entre esse conjunto e a superfície onde o movimento acontece. Observando o diagrama de corpo livre:

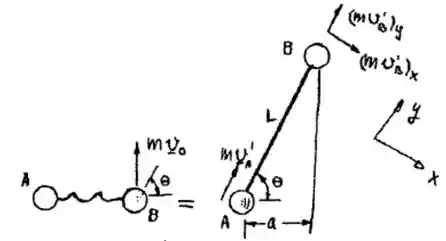
Como as esferas tem a mesma massa, assim m A = m B = m . Como elas estão conectadas por uma corda, a quantidade de movimento total é conservada. Assim temos:

∑ m v i n i c i a l = ∑ m v f i n a l

E m   x :   - m v 0 cos ⁡ θ = m v B ' x

E m   y :     m v 0 sin ⁡ θ = m v A ' + m v B ' y

Passo 2

Como a corda é inextensível, temos que v A ' = v B ' y . Logo, para a direção y temos:

v 0 sin ⁡ θ = 2 v A '

v 0 L 2 - a 2 L = 2 v A ' → v A ' = v 0 2 L L 2 - a 2

v B ' y = v 0 2 L L 2 - a 2  

Para x temos:

v B ' x =   - v 0 cos ⁡ θ =   - v 0 a L

Assim, a intensidade da velocidade da esfera B é:

v B ' =   v B ' x 2 + v B ' y 2 =   - v 0 a L 2 + v 0 2 L L 2 - a 2   2

v B ' = v 0 a 2 L 2 + L 2 - a 2 4 L 2 = v 0 2 L L 2 + 3 a 2

Passo 3

Agora vamos calcular a energia perdida quando a corda fica tensionada. Para o momento inicial, a energia cinética do conjunto é:

T = 1 2 m v 0 2

Quando a corda fica tensionada, temos que a energia cinética das esferas são:

T ' = 1 2 m v A ' + 1 2 m v B '

T ' = 1 2 m v 0 2 L L 2 - a 2 + 1 2 m v 0 2 L L 2 + 3 a 2 = 1 2 m v 0 2 4 L 2 ( 2 L 2 + 2 a 2 )

T ' =   m v 0 2 4 L 2 ( L 2 + a 2 )

Assim, a energia perdida é:

Δ T = T - T ' = 1 2 m v 0 2 -   m v 0 2 4 L 2 ( L 2 + a 2 )

Δ T = m v 0 2 4 L 2 ( L 2 - a 2 )

Resposta

  1. v A ' = v 0 2 L L 2 - a 2 , v B ' = v 0 2 L L 2 + 3 a 2

  2. Δ T = m v 0 2 4 L 2 ( L 2 - a 2 )
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um homem parado em um elevador que se move com uma aceleração constante, segura um bloco B de 3 kg entre dois outros blocos de tal forma que o movimento de B em relação a A e C é iminente. Sabendo que
As hélices de um navio de peso W podem produzir uma força propulsora Fo; eles produzem uma força de mesma magnitude, mas de direção oposta quando os motores são invertidos. Sabendo que o navio estava
As caixas A e B estão paradas em uma esteira que está inicialmente em repouso. A correia é repentinamente iniciada em uma direção para cima de modo que o deslizamento ocorra entre a correia e as caixa
Um jogador de hockey bate no disco de maneira que este chega ao repouso 9 s depois de ter escorregado 30 m sobre o gelo. Determine (a) a velocidade inicial do disco e (b) o coeficiente de atrito entre
Uma embalagem está em repouso em uma correia transportadora, que inicialmente está em repouso. A correia é acionada e se move para a direita por 1,3s com uma aceleração constante de 2 m/ s 2 . A corre