Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 89

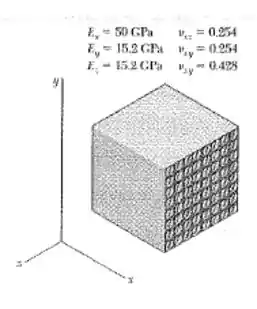
Um cubo, de um material compósito, com 40 mm de lado e as propriedades mostradas na figura é feito de polímeros com fibras de vidro alinhadas na direção x. O cubo é impedido de se deformar nas direções y e z e está submetido a uma força de tração de 65 kN na direção x. Determine (a) a variação na dimensão do cubo na direção x e (b) as tensões σ x ,   σ y   e   σ z .

Passo 1

Nós temos do enunciado

E x = 50   G P a

E y = 15,2   G P a

E Z = 15,2   G P a

v x z = 0,254

v x y = 0,254

v z y = 0,428

Essa questão é um pouco mais complexa. As equaç~es que vamos ter para montar um sisteminha serão

1   ϵ x = σ x E x - v y x σ y E y - v z x σ z E z

2   ϵ y = - v x y σ x E x + σ y E y - v z y σ z E z

3 ϵ z = - v x z σ x E x - v y z σ y E y + σ z E z

Temos ainda que

4 v x y E x = v y x E y

5 v y z E y = v z y E z

6 v z x E z = v x z E x

Passo 2

Do enunciado temos que o cubo é impedido de se deformar nas direções y e z, logo

ϵ y = 0   e   ϵ z = 0

Aplicand essascontições em (2) e (3).

7 1 E y σ y - v z y E z σ z = v x y E x σ x

8 - v y z E y σ y + 1 E 2 σ z = v x z E x σ x

Aplicando os valores que nos foram dados no enunciado temos

1 15,2 σ y - 0,428 15,2 σ z = 0,254 50 σ x → σ y - 0,428 σ z = 0,077216 σ x

- 0,428 15,2 σ y + 1 15,2 σ z = 0,254 50 σ x → - 0,428 σ y + σ z = 0,077216 σ x

Com essa duas equações encontramos que

σ y - 0,428 σ z = → - 0,428 σ y + σ z

Logo, σ y = σ z , com isso

σ y - 0,428 σ z = 0,077216 σ x

σ y - 0,428 σ y = 0,077216 σ x

0,572 σ y = 0,077216 σ x

σ y = σ z = 0,077216 σ x

Passo 3

Usando agora as equações (4) e (5) na (1) temos

ϵ x = 1 E x σ x - v x y E x σ y - v x z E x σ z

ϵ x = 1 E x 1 - 0,254 0,134993 - 0,254 0,134993 σ x

ϵ x = 0,93142 σ x E x

Passo 4

Calculando a área da seção que estamos trabalhando temos

A = l 2

por ser um cubo.

A = 40 2 = 1600 m m 2 = 1600 × 10 - 6 m 2

σ x   é dado por

σ x = P A = 35 × 10 3 1600 × 10 - 6 = 40,625 × 10 6   P a

Nosso ϵ x então será

ϵ x = 0,93142 σ x E x

ϵ x = 0,93142 ( 40,625 × 10 3 ) 50 × 10 9 = 756,78 × 10 - 6

Passo 5

Para responder a letra (a) então teremos

δ x = L x ϵ x = 40 m m 756,78 × 10 - 6 = 0,0303   m m

E para a (b) teremos

σ x = 40,625 × 10 6 P a = 40,6   M P a

σ y = σ z = 0,134993 40,625 × 10 6 = 5,48 × 10 6 P a = 5,48   M P a

Resposta

δ x = 0,0303   m m

σ x = 40,6   M P a

σ y = σ z = 5,48   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a barra composta do P r o b .2.10 6 , determinar a tensão residual em cada lâmina, se P cresce gradualmente desde zero até 357k N e então, decresce até zero.
Para a barra composta do P r o b .2.104 , determinar a tensão residual em cada porção da barra, se P cresce gradualmente desde zero até a deflexão do ponto C atingir um valor máximo δ m e então decres
Uma barra de aço de comprimento L e seção transversal uniforme de área A , está fixada na extremidade a dois suportes rígidos e ausente de tensões a uma temperatura de 20 ° C . o aço é assumido ser el
Para a barra composta do P r o b .2.10 6 , determinar a tensão residual em cada lâmina, se P cresce gradualmente desde zero até a deformação da barra atingir um valor máximo δ m e então decresce até z
A barra ACB é engastada aos suportes rígidos e está ausente de tensões a uma temperatura de 2 5 ° C . O aço é assumido elastoplástico com E = 200G P a e σ e = 250M P a . A temperatura de ambas as porç