Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 88

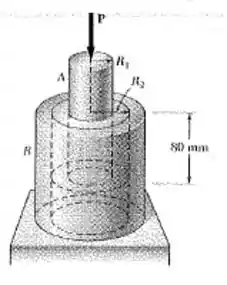
Um suporte isolado de vibrações consiste em uma barra A de raio R 1 e um tupo B de raio interno R 2 ,   colado a um tubo de borracha de 80 mm de comprimento com um módulo de elasticidade transversal G = 10,93   M P a .   Determine o valor necessário para a relação R 2 / R 1 , se uma força P de 10 kN provocar um deslocamento de 2 mm da barra A.

Passo 1

Para essa questão teremos nosso r variando entre R 1   e   R 2

R 1 ≤ r ≤ R 2

τ vai ser dado por

τ = P A = P 2 π r h

Onde

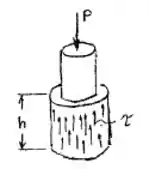
Passo 2

Vamos ter ainda que

t g γ ≈ γ = τ G

Substituindo a relação anterior

γ = P 2 π G h r

A deformação será dada por

d δ d r = γ

Onde

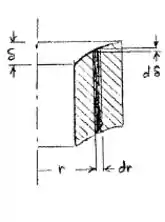
Com isso temos

d δ = γ d r

d δ = P 2 π G h r d r

Passo 3

Aplicando a integral dos dois lados temos que a deformação total será dada por

δ = ∫ R 1 R 2 d δ = P 2 π G h r ∫ R 1 R 2 1 r   d r

P 2 π G h r ln ⁡ r | R 2 R 1 = P 2 π G h r l n R 2 - l n R 1

δ = P 2 π G h r ln ⁡ R 2 R 1

Passo 4

Dados que

h = 80   m m = 0,08   m m

G = 10,93 × 10 6   P a

δ = 2 × 10 - 3   m

P = 10   k N

Vamos simplesmente reescrever esses valores na fórmulinha que desenvolvemos e encontrar o valor da relação R 2 / R 1 . Mas antes, pra manter uma organização, vamos isolar o R 2 / R 1 .

δ = P 2 π G h r ln ⁡ R 2 R 1

ln ⁡ R 2 R 1 = 2 π G h δ P

Substituindo então os valores na fórmula

ln ⁡ R 2 R 1 = 2 π 10,93 × 10 6 0,08 2 × 10 - 3 10 × 10 3 = 1,0988

ln ⁡ R 2 R 1 = 1,0988

Aplicando exponencial dos dois falos temos

e ln ⁡ R 2 R 1 = e 1,0988

R 2 R 1 = 3,00

Resposta

R 2 R 1 = 3,00

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Resolver o P r o b .2.118 , considerando que a temperatura da barra é elevada para 150 ° C e então retorna para 25 ° C .
Para a barra composta do P r o b .2.104 , determinar a tensão residual em cada porção da barra, se P cresce gradualmente desde zero até 1080k N e então decresce até zero.
A linha de inclinação b:a, onde a e b são ambas diferentes de zero, estava desenhada na placa quando ela estava ausente de tensões. A placa é então submetida ao estado biaxial de tensões indicado. Ped
Usando E = 200G P a , determinar o módulo de resiliência para cada um dos tipos de aço estrutural seguintes:ASTM A-36; σ e = 250M P a ASTM A-441; σ e = 320M P a ASTM A-514; σ e = 690M P a
Determinar o módulo de resiliência para cada uma das seguintes ligas:Monel (trabalhado a frio): E = 180G P a ; σ e = 585M P a Monel (recozido): E = 180G P a ; σ e = 220M P a Liga de titânio: E = 115G