Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 92

O cubo do Problema 2.91, de um material compósito, é impedido de se deformar na direção z e é alongado na direção x em 0,035 mm por uma força de tração na direção x. Determine (a) as tensões σ x ,     σ y ,     σ z e (b) a variação na dimensão do cubo na direção y.

Passo 1

Fala aí gurizada tudo belezinha??? O enunciado pede a variação na dimensão do cubo na direção x primeiramente vamos determinar as equações de deformação nas três direções:

ε x = σ x E x - v y x σ y E y - v z x σ z E z

ε y = - v x y σ x E x + σ y E y - v z y σ z E z

ε z = - v x z σ x E x - v y z σ y E y + σ z E z

Igualando as equações em funções das direções fornecidas no enunciado temos:

v x y E x = v y x E y

v y z E y = v z y E z

v z x E s = v x z E x

Condição de restrição: ε z = 0 ,

Condição de carga:

σ z = - v x z E x σ x + 1 E z σ z σ z = v z y E z E x σ x = 0,254   x   ( 15,2 ) 50 = 0,077216 σ x

Passo 2

As condições de restrição são fornecidas no passo 1 temos que:

ε x = 1 E x σ x - v z y E z σ z = 1 E x σ x - v x z E x σ z = 1 E x σ x - 0,254   σ z = 1 E x [ 1 - 0,254   x   ( 0,077216 ) σ x = 0,98039 E x σ x σ x = E x ε x 0,98039

Vamos relembrar o elemento do enunciado com seus respectivos valores:

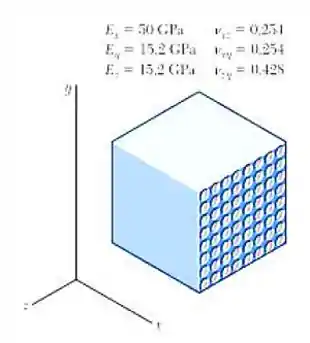
Mas a deformação é obtida, de tal maneira:

ε x = δ x L x = 0,035   m m 40   m m = 875   x   10 - 6

Então agora podemos determinar tensões σ x ,     σ y ,     σ z e (b) a variação na dimensão do cubo na direção y respectivamente

a   σ x = 50   x   10 9   x   875   x   10 - 6 0,98039 = 44,625   x   10 3 P a σ z = 0,077216   x   44,625   x   10 6 = 3,446   x   10 6 P a

Antes de determinarmos a variação na dimensão precisamos determinar a deformação , venham comigo !!!

ε y = v x y E x σ x + 1 E y σ y - v z y E z σ z = - 0,254   x   44,625   x   10 6 50   x   10 9 + 0 - 0,428   x   3,446   x   10 6 15,2   x   10 9 = - 323,73   x   10 - 6

b δ y = L y ε y = 40   m m   x   - 323,73   x   10 - 6

Resposta

a σ x = 44,6   M P a σ y = 0 σ z = 3,45   M P a

b δ y = - 0,0129   m m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois blocos de borracha com um módulo de elasticidade transversal G = 12M P a são colados a dois suportes rígidos e a uma placa AB. Sabendo que c = 100m m eP = 45k N , determine as menores dimensões a
As constantes de material E, G, k e v estão relacionadas nas Equações (2.24) e (2.34). mostre que qualquer uma dessas constantes pode ser expressa em função de quaisquer outras duas constantes. Por ex
Para o apoio do elastômero do Problema 2.79 com b = 10 i n . ea = 1 i n . determine o módulo de cisalhamento G e a tensão de cisalhamento τ para uma força lateral máxima P = 5k i p s e um deslocamento
Uma esfera solida de aço com diâmetro de 152,4 mm é mergulhada no oceano, em um ponto onde a pressão é de 49 MPa (aproximadamente 4,8 km abaixo da superfície). Sabendo que E = 200G P aev = 0,30 , dete
Uma unidade de isolamento de vibrações consiste em dois blocos de borracha dura colados a uma placa AB e a suportes rígidos conforme mostrado. Sabendo que a intensidade da força P = 25k N produz uma d