Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 2.Problemas - Ex. 91
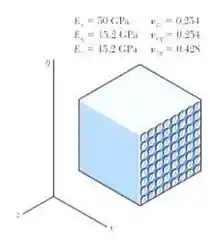
Um cubo, de um material compósito, com 40 mm de lado e as propriedades mostradas na figura é feito de polímeros com fibras de vidro alinhadas na direção x. O cubo é impedido de se deformar nas direções y e z e está submetido a uma força de tração de na direção x. Determine (a) a variação na dimensão do cubo na direção x e (b) as tensões .
Passo 1
Fala aí gurizada tudo belezinha??? O enunciado pede a variação na dimensão do cubo na direção x primeiramente vamos determinar as equações de deformação nas três direções:
Igualando as equações em funções das direções fornecidas no enunciado temos:
Passo 2
As condições de restrição são fornecidas no passo 1 temos que:
(1) (2)
Vamos relembrar o elemento do enunciado com seus respectivos valores:
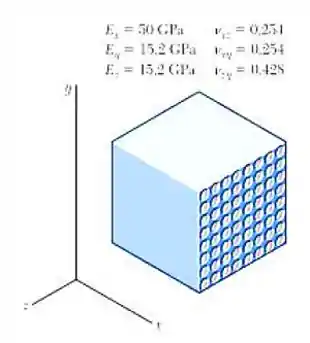
Substituindo os valores em 1 e 2 temos:
Resolvendo simultaneamente,
Considerando a equação de deformação abaixo e modulo abaixo, substituindo os valores do enunciado temos:
Passo 3
Antes de encontrarmos a tensão e a deformação precisamos determinar a área do elemento, então temos:
Agora sim podemos determinar a tensão e a deformação , vejam :D
Passo 4
Feito isso podemos determinar a variação na dimensão do cubo na direção x e (b) as tensões .