Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 61

Uma cunha de 15° é forçada por baixo de um tubo de 50 kg, tal como mostra a figura. Sabendo que o coeficiente de atrito estático nas superfícies da cunha é 0,20, determine o maior coeficiente de atrito estático entre o tubo e a parede vertical para que o escorregamento seja iminente em A.

Passo 1

Vamos começar esse excercício desenhando o diagrama de corpo livre para o tubo:

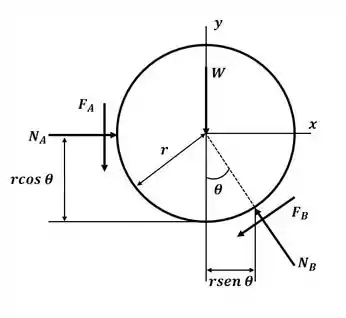
Sabemos que as forças de atrito podem ser escritas como:

F A = μ s N A

F B = μ s N B

Agora vamos calcular o somatório de momento do sistema em relação ao ponto A:

+ ↺ ∑ M A = 0

N B r c o s θ - μ B N B - μ B N B s e n θ r - W r = 0

Simplificando r e colocando N B em evidência:

N B c o s θ - μ B 1 + s e n θ = W → N B = W c o s θ - μ B ( 1 + s e n θ )

Agora, susbtituindo os valores para μ B e θ dados no enunciado:

N B = W c o s 15 ° - 0,2 ( 1 + s e n 15 ° ) → N B = 1,4 W

Passo 2

Agora vamos aplicar o somatório na direção do eixo x :

+ → ∑ F x = 0

N A - N B s e n θ - μ B N B c o s θ = 0 → N A = N B ( s e n θ + μ B c o s θ )

Substituindo o valor encontrado para N B :

N A = 1,4 W s e n 15 ° + 0,2 c o s 15 ° → N A = 0,633 W

Agora vamos aplicar o somatório de forças na direção y :

+ ↑ ∑ F y = 0

- F A - W + N B c o s θ - μ B N B s e n θ = 0 → F A = N B c o s θ - μ B s e n θ - W

Substituindo o valor encontrado para N B :

F A = 1,4 W c o s 15 ° - 0,2 s e n 15 ° - W → F A = 0,28 W

Passo 3

Agora, se o tubo escorregar em A, teremos a força de atrito sendo dada por:

F A = μ A N A

Então, substituindo os valores encontrados para N A e F A :

0,28 W = μ A 0,633 W → μ A = 0,442

Resposta

μ A = 0,442

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um esticador, semelhante ao mostrado na F i g u r a8.17 , é usado para tracionar o elemento ABda treliça. O coeficiente de atrito estático entre os parafusos com rosca quadrada e o esticador é μ s = 0
Se uma força horizontal P=100N for aplicada perpendicularmente ao cabo da manivela em A , determine a força compressiva F exercida sobre o material. Cada rosca quadrada tem diâmetro médio de 25m m e a
Determine a força de aperto na placa A se o parafuso do grampo “ C ” for apertado com um torque de M = 8N ⋅ m . O parafuso de rosca quadrada tem raio médio de 10m m , avanço de rosca de 3m m e coefici
O mecanismo de freio consiste em dois braços com pinos e um parafuso de rosca quadrada comroscas esquerda e direita. Assim, quando girado, o parafuso aproxima os dois braços. Se o avanço do parafuso é
Se forças de binário F = 35N forem aplicadas ao punho da morsa, determine a força compressiva desenvolvida no bloco. Desconsidere o atrito no mancal A . A guia em B é lisa. O parafuso de rosca quadrad