Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 4.Problemas - Ex. 83
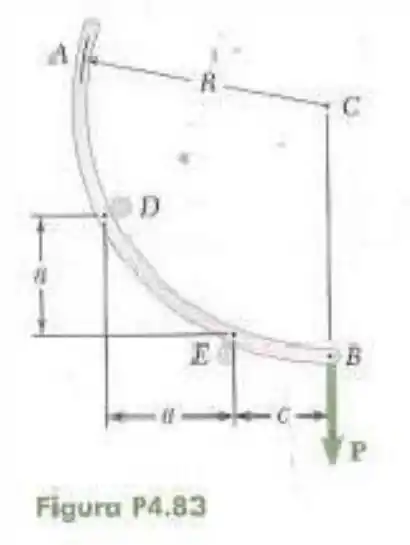
83- A haste está curvada no formato de um arco de círculo e alojada entre dois pinos e . A haste sustenta uma carga na extremidade . Desprezando o atrito e o peso da haste, determine a distância correspondente a condição de equilíbrio quando e .
Passo 1
Quando há uma força em puxando o arco para baixo surge no arco as seguintes reações em e .
Onde e
Pela lei dos cossenos temos que vale:
Passo 2
Porém se analisarmos de outra maneira temos o seguinte desenho:
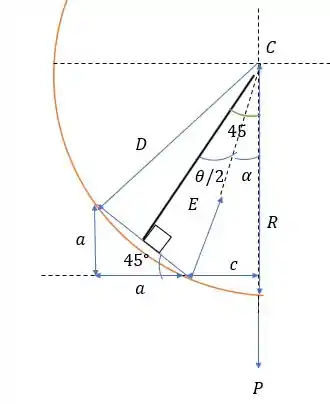
Logo será:
Então será:
Problema inteiramente geométrico.
Resposta
Exercícios de Livros Relacionados
Sabendo que a estrutura mostrada na figura tem um fio em B de a = 13 m m , determine a força P necessária para manter o equilíbrio na posição mostrada.
Sabendo que a estrutura mostrada na figura tem um fio em B de a = 25 m m , determine a força P necessária para manter o equilíbrio na posição mostrada.
A tesoura para poda mostrada na figura consiste em duas lâminas e dois cabos. Os dois cabos da ferramenta estão ligados pelo pino C , e as duas lâminas estão ligadas pelo pino D . A lâmina da esquerda
Determine a intensidade das forças de aperto exercidas ao longo da linha a a sobre a porca quando se aplicam duas forças de 225 N nos cabos da ferramenta, tal como mostra a figura. Suponha que os pino
O movimento da pá carregadeira da retroescavadeira mostrada na figura é controlado pelos cilindros hidráulicos A D ,C GeE F . Para cada tentativa de retirar uma parte do calçamento, uma força P de 9 k