Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 124
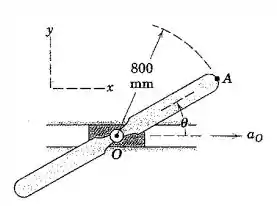
Com referencia às hélices e o bloco deslizante do mancal do Prob. 5/123 onde Se e quando, encontre a aceleração do ponto A para esse instante.
Passo 1
Este exercício é uma continuação do anterior com algumas modificações. Agora, existe aceleração angular Portanto, o termo da aceleração relativa tangencial não será nulo.
Além disso, , logo o termo da aceleração relativa normal será nulo.
Relembrando que:
É a aceleração relativa tangencial e ela é perpendicular à distância AO.
Ah, a questão pede apenas o módulo, então não vamos nos preocupar com notação vetorial.
Passo 2
Vamos então resolver para , pedido na questão.
Representando o diagrama de vetores:
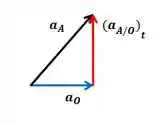
Podemos resolver por Pitágoras:
Resposta
Exercícios de Livros Relacionados
A viga de aço de 9m está sendo levantada a partir de sua posição horizontal pelos dois cabos presos em A e B. Se as acelerações angulares iniciais dos tambores de elevação são α 1 = 0,5r a d / s 2 e α
No instante mostrado, a bola B está rolando ao longo da ranhura no disco com uma velocidade de 600mm/s e uma aceleração de 150mm/s2, ambas medidas em relação ao disco e dirigidas para longe de O. Se n
A bola C se desloca com uma velocidade de 3 m/s, que está aumentando a uma taxa constante de 1,5 m/s2, ambas medidas em relação à placa circular e direcionadas como mostrado. No mesmo instante, a plac
A bola C se desloca ao longo da ranhura de A para B com uma velocidade de 0,9 m/s e aceleração de 0,45 m/s2, ambas medidas em relação à placa circular. Nesse mesmo instante, a placa gira com a velocid
Determine a velocidade angular e acelaração angular da placa CD do mecanismo triturador de pedras no instante em que AB está na horizontal. Neste instante, θ = 30 ° e ϕ = 90 ° . O membro de acionament