Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 161

Um veiculo experimental A viaja com velocidade constante v em relação à Terra ao longo de uma estrada de ferro ligando norte ao sul. Determine a aceleração de Coriolis a c o r em função da latitude θ . Assuma um referencial que gira fixo na Terra Bxyz e a Terra esférica. Se a velocidade do veículo é v = 500   k m / h , determine o modulo da aceleração de Coriolis (a) no equador e (b) no polo norte.

Passo 1

Vamos desenhar a Terra em 2D para ficar mais fácil a visualização do problema.

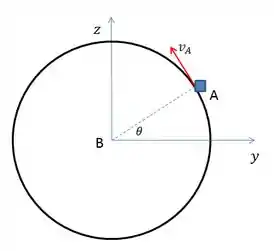
Um dado fundamental para a resolução do problema é a velocidade angular (velocidade de rotação) da Terra, que pode ser obtida pela tabela D/2.

ω = 7,292 × 10 - 5 k ^   r a d / s

Pronto, beleza! Agora vamos parametrizar a velocidade de A em relação aos eixos z e y.

v A = 500 3,6 - s e n θ   j ^ + c o s θ   k ^ = 138,89 - s e n θ   j ^ + c o s θ   k ^ m / s

Lembrando que a aceleração de Coriolis é dada pela equação:

a C o r = 2 ω × v r e l

Onde v r e l = v A neste caso, pois o veículo está na Terra. Temos então que:

a C o r = 2 7,292 × 10 - 5 k ^ × 138,89 - s e n θ   j ^ + c o s θ   k ^

a C o r = 0,0203 s e n θ   i ^   m / s 2

Passo 2

Na letra (a) é pedida a aceleração de Coriolis no Equador ( θ = 0 ) :

a C o r = 0,0203 s e n 0 = 0

Na letra (b) é pedida a aceleração de Coriolis no Polo Norte ( θ = 90 ° ) :

a C o r = 0,0203 s e n 9 0 ° = 0,0203   i ^   m / s 2

Resposta

  1. a C o r = 0
  2. a C o r = 0,0203   i ^   m / s 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A lança do guindaste AO gira em torno dp eixo z com uma velocidade angular constante w 1=0,15r a d / s , enquanto ela está girando para baixo com uma velocidade angular constante w 2=0,2r a d / s . De
No instante mostrado, o guindaste da torre gira em torno do eixo z com uma velocidade angular ω 1 = 0,25r a d / s , a qual está aumentando a 0,6r a d / s ² ². A lança do guindaste AO gira para baixo c
Se a engrenagem de cima B gira a uma taxa constante ω , determine a velocidade angular da engrenagem A, que está livre para girar em torno do eixo e rola sobre a engrenagem fixa de baixo C.
O telescópio está montado sobre uma estrutura F que permite ser direcionado para qualquer ponto do céu. No instante θ = 30 ° , a estrutura tem uma aceleraçãoαy = 0,2r a d / s 2 e uma velocidade angula
A engrenagem C é movida pelo eixo DE, enquanto a engrenagem B gira livremente de seu eixo GF, o qual realiza uma precessão livremente em torno do eixo DE. Se a engrenagem A é acionada com uma velocida