Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.7 - Ex. 167

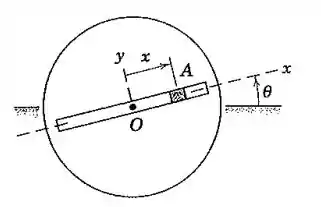
O cursor A oscila na ranhura em torno da posição neutra O com uma frequência de dois ciclos por segundo e uma amplitude x m a x = 50 m m de modo que o seu deslocamento em milímetros pode ser escrito x = 50 s e n 4 π t onde t é o tempo em segundos. O disco, por sua vez, é posto em oscilação angular em torno de O com uma frequência de quatro ciclos por segundo e uma amplitude θ = 0,20 s e n 8 π t . Calcule a aceleração de A para as posições (a) x = 0 ,   c o m   x ˙   p o s i t i v o   e   b x = 50 m m .

Passo 1

Bom galera, vamos apresentar os dados da questão.

x = 50 s e n 4 π t

Podemos encontrar sua velocidade v r e l e aceleração a r e l pela derivada da posição:

x ˙ = v r e l = 200 π c o s 4 π t   m / s

x ¨ = a r e l = - 800 π 2 s e n 4 π t   m / s 2

Da mesma forma, vamos fazer para o deslocamento angular do disco:

θ = 0,20 s e n 8 π t

θ ˙ = ω = 1,6 π c o s 8 π t   k ^   r a d / s

θ ¨ = α = - 12,8 π 2 s e n 8 π t   k ^   r a d / s 2

Passo 2

Nesta etapa vamos calcular a aceleração de A para x = 0:

Quando x = 0, então também temos que t = 0. Vamos ver o porquê pela equação de posição:

0 = 50 s e n 4 π t → 4 π t = 0 → t = 0

Com isso, vamos à equação de aceleração:

a A = a O + α × r A O + ω × ω × r A O + 2 ω × v r e l + a r e l

a A = 0 + - 12,8 π 2 s e n 0   k ^   × 50 s e n 0   i ^ - 1,6 π c o s 0 2 50 s e n 0   i ^ + 2 1,6 π c o s 0 k ^ × 200 π c o s 0   i ^ - 800 π 2 s e n 0   i ^

a A = 2 1,6 π c o s 0 k ^ × 200 π c o s 0   i ^ = 6320   j ^   m m / s 2

a A = 6,32 j ^   m / s 2

Passo 3

Para resolver a letra (b), basta usar a mesma metodologia da letra (a). Neste caso, x = 50 mm: 50 = 50 s e n 4 π t → 1 = s e n 4 π t → 4 π t = π 2 → t = 1 8 s

Com isso, vamos à equação de aceleração:

a A = a O + α × r A O + ω × ω × r A O + 2 ω × v r e l + a r e l

a A = 0 + - 12,8 π 2 s e n ( π )   k ^   × 50 s e n ( π / 2 )   i ^ - [ 1,6 π c o s ( π ) ] 2 50 s e n ( π / 2 )   i ^ + 2 1,6 π c o s ( π ) k ^ × 200 π c o s ( π / 2 )   i ^ - 800 π 2 s e n ( π / 2 )   i ^

a A = - [ - 1,6 π ] 2 50   i ^ - 800 π 2   i ^

a A = - 9160   i ^   m m / s 2

a A = - 9,16   i ^   m / s 2

Resposta

  1. a A = 6,32 j ^   m / s 2
  2. a A = - 9,16   i ^   m / s 2
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No instante mostrado, o eixo gira com uma velocidade angular ω p = 6r a d / s e uma aceleração angular ω ˙ p = 3r a d / s 2 . No mesmo instante, o disco gira em torno de seu eixo com uma velocidade an
O disco A gira a uma velocidade angular constante de 10r a d / s . Se a barra B C está ligada ao disco e ao anel por juntas esféricas, determine a velocidade do anel B no instante mostrado. Além disso
Resolva o exemplo 20.5 fixando os eixos x , y , z àbarra B D de maneira que Ω = ω 1 + ω 2 . Neste caso, o anel parece se deslocar apenas radialmente para fora ao longo de B D ; por conseguinte,Ω x y z
A placa triangular A B C está apoiada em A por uma junta esférica e em C pelo plano x - z . O lado A B encontra-se no plano x - y . No instante θ = 60 ° , θ ˙ = 2r a d / s , θ ¨ = 3r a d / s 2 e o pon
Resolva o exemplo 20.5 tal que os eixos x , y , z se desloquem com uma translação curvilínea, Ω = 0 no caso em que o anel parece ter uma velocidade angular Ω x y z = ω 1 + ω 2 e um movimento radial.