Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 43

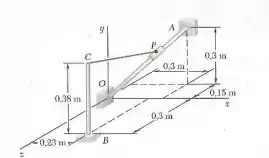
O cursor P pode mover-se ao longo da barra OA. Uma corda elástica PC é ligada ao cursor e ao elemento vertical BC. Sabendo que a distância de O até P é 0.15 m e que a tração na corda é 13 N, determine (a) o ângulo entre a corda elástica e a barra AO, (b) a projeção sobre AO da força exercida pela corda PC no ponto P.

Passo 1

Falaaaaaa pessoal, show de bola??

Bora resolver esse exercício na maciotaaaaa, então siimboraa!!

Primero note

O A = 0.3 2 + 0.3 2 + - 0.15 2 = 0.45   m

λ O A = O A O A = 1 0.45 0.3 i + 0.3 j - 0.15 k

λ O A = 1 3 2 i + 2 j - k

O P = 0.15

O P = 1 3 ( O A )

Para as coordenadas no ponto P, temos ( 0.1 i ,   0.1 j ,   - 0.05 )

P C ¯ = 0.13 m i + 0.28 m j + 0.35   m k

P C = 0.13 2 + 0.28 2 + 0.35 2 = 0.2178

Passo 2

  1. Onde P C ¯ ⋅ λ O A = P C cos ⁡ θ

    2. 0.13 i + 0.28 j + 0.35 k ⋅ 1 3 2 i + 2 j - k = 0.2178 cos ⁡ θ

    cos ⁡ θ = 1 3 0.2178   0.13 ⋅ 2 + 0.28 ⋅ 2 + 0.35 ⋅ - 1

    cos ⁡ θ = 0.335697

    θ = 70.39 °

    Passo 3

  2. Onde

T P C O A = T P C ⋅ λ O A

= T P C λ P C ⋅ λ O A

= T P C ⋅ P C P C ⋅ λ O A

= T P C cos ⁡ θ

= 13 ⋅ 0.335697

T P C O A = 4.36   N

Resposta

  1. θ ≅ 70.40
  2. T P C O A ≅ 4.36   N
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Expresse F → vetorialmente em termos dos vetores unitários i ^ , j ^ , k ^ . Determine o ângulo entre F → e o eixo y .
Determine as componentes da força que atuam paralela e perpendicularmente ao eixo do poste.
iv)
iii)