Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 1.9 - Ex. 1iv

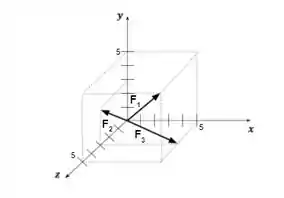
iv)

Passo 1

Neste caso, primeiro devemos escrever os vetores de acordo com as coordenadas do plano cartesiano, F=(x,y,z)

F_1 = (5,5 , 5) -> F_2 = (0,3 , 3) -> F_3 = ( 5,0 , 3 )

A resultante se dá pelo somatório vetorial de todas as forças, sendo assim temos:

R = sum_(i = 1)^n F_i

R_x = (5 + 0 + 5) = 10 k N

R_y = (5 + 3 + 0) = 8 k N

R_z = (5 + 3 + 3) = 11 k N

Passo 2

Já os cossenos diretores se dão, pela fórmula abaixo:

cos theta_x = (x)/(|R|)

cos theta_y = (y)/(|R|)

cos theta_z = (z)/(|R|)

Sendo assim, ao substituirmos teremos:

cos theta_x = (10)/(sqrt(( 10 )^2 + (8)^2 + (11)^2)) -> cos theta_x = (10)/(sqrt(285)) tildetilde 0,59

cos theta_y = (8)/(sqrt((10)^2 + (8)^2 + (11)^2)) tildetilde 0,47

cos theta_z = (11)/(sqrt((10)^2 + (8)^2 + (11)^2)) tildetilde 0,65

Resposta

1.iv) R = ( 10,8 , 11 ) ; 0,59; 0,47;0,65

Exercícios de Livros Relacionados

Determine a intensidade da projeção da força F 1 ao longo do cabo A C .
Determine a componente projetada da força de 80N que atua ao longo do eixo A B do tubo.
Determine a intensidade da projeção da força F = 600N ao longo do eixo u .
Se a força F = 100N se encontra no plano D B E C , que é paralelo ao plano x - z e forma um ângulo de 10 ° com a linha estendida D B , conforme mostra a figura, determine o ângulo que F forma com a di
Os dois cabos exercem as forças sobre o poste mostradas na figura. Determine a intensidade da componente projetada de cada força que atua ao longo do eixo OA do poste.