Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.7 - Ex. 99

Expresse vetorialmente em termos dos vetores unitários , , . Determine o ângulo entre e o eixo .

Passo 1

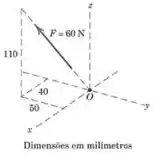
Muito cuidado aqui: as medidas que foram dadas na figura não são as componentes da força naquelas direções. Mas podemos usá-las para encontrar o vetor unitário naquela direção!

Vamos chamar esse vetor de :

A ideia aqui é que estamos tomando um vetor que tem exatamente aquelas dimensões e divindo pelo seu módulo, para achar o vetor unitário na mesma direção:

E agora para encontrar o vetor é só multiplicar por :

Passo 2

E agora queremos o ângulo que o vetor forma com o eixo . Podemos usar a definição do produto escalar para calcular isso:

Vamos olhar primeiro para o lado esquerdo da equação, é a projeção de no eixo , que nós já calculamos no passo acima:

E olhando para o lado direito:

Então:

Pronto!

Resposta

e o ângulo que forma com o eixo é .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A força F → tem um módulo de 900N e atua ao longo da diagonal do paralelepípedo, como mostrado. Expresse F → em termos de seu módulo multiplicado pelo vetor unitário apropriado, e determine seus compo

A torre de transmissão de microondas com 70m de altura é equilibrada por três cabos de amarração, como mostrado. O cabo A B suporta uma força trativa de 12k N . Expresse em forma vetorial a força corr

Expresse F → como um vetor em termos dos vetores unitários i ^ , j ^ e k ^ . Determine a projeção de F → , tanto como um escalar quanto como um vetor, sobre a linha O A , que está situada no plano x -

Expresse a força F → como um vetor em termos dos vetores unitários i ^ , j ^ e k ^ . Determine os ângulos θ x , θ y e θ z que F → faz com os eixos positivos x , y e z .

A força trativa no cabo de sustentação A B vale 10k N . Escreva, como um vetor T → , a força que o cabo exerce sobre a haste B C . Determine os ângulos θ x , θ y e θ z que a linha de ação de T → faz c