Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 10.Problemas - Ex. 52
Deduza uma expressão para a eficiência mecânica do macaco discutido na Seção 8.6. Mostre que, se o macaco tem que ser autotravante, a eficiência mecânica não pode exceder .
Passo 1
Primeiro vamos entender o problema! Na seção 8.6, temos a seguinte figura, que usaremos como base para mostrar o que a questão pede.
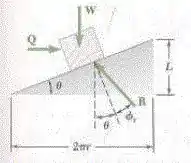
Note que, as forças atuando no macaco forma um triângulo. De tal modo que, a força Q e a força W formam um ângulo de 90° e o ângulo entre W e R é .
Passo 2
Logo podemos tirar algumas relações. Então:
Lembre-se que, temos dois tipos de trabalho o trabalho de entrada dado por Q e o trabalho de saída dado por W. Logo vamos analizar o trabalho de entrada.
Se tiver achando um pouco complicado dê uma lida novamente da Secão 8.6. Que vai da certo! Voltando para o trabalho de entrada, que é dado por:
Certo, o trabalho de entrada foi tranquilo, o trabalho de saída é só atentarmos para outra relação, de modo que:
Então o trabalho de saída que é dado por:
Torna-se:
Portano a eficiência que é o trabalho de saída pelo trabalho de entrada é:
Passo 3
Já estamos quase terminando! Mas antes, vamos lembrar que se o conector é de travamento automático então:
Somando de ambos os lados temos:
Aplicando tangente em ambos os lados:
Do passo anterior sabemos que:
Se substituirmos o denominador, teremos a desigualdade:
Passo 4
Certo! Agora lembre-se de uma igualdade trigonométrica,
Substituindo na desisgualdade teremos:
Simplificando:
Portanto:
Resposta
Ei, a resposta está no passo a passo :)