Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.7 - Ex. 166
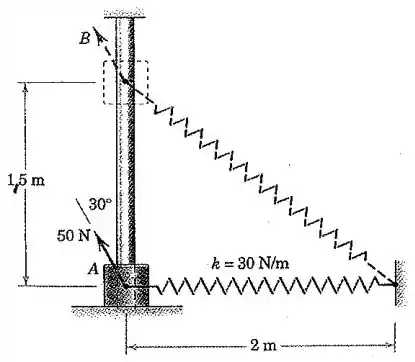
O cursor tem uma massa de e está preso à mola leve, que tem uma rigidez de e um comprimento sem deformação de . O cursor é liberado a partir do repouso em e desliza para cima na barra lisa sob a ação da força constante de . Calcule a velocidade do cursor quando este passa a posição .
Passo 1
O trabalho da força altera a energia mecânica total do sistema, de modo que podemos escrever:
Vamos calcular cada um desses termos separadamente:
Passo 2
Para calcular a variação de energia potencial elástica , primeiramente vamos determinar os valores das deformações e . Como o comprimento natural da mola é de , temos:
Para calcular , usamos o teorema de Pitágoras:
Então:
Passo 3
Retornando à equação de conservação de energia, temos:
Resposta
Exercícios de Livros Relacionados
O elevador de carga e a carga têm massa total de 800 kg, e o contrapeso C tem massa de 150 kg. Em um dado instante, o elevador tem uma velocidade para cima de 2 m/s e uma aceleração de 1,5 m/s2. Deter
Resolva o Problema 18.12 usando a equação de conservação de energia.
Resolva o Problema 18.5 usando a equação de conservação de energia.
Se o disco de 30k g é solto do repouso quando θ = 0 ° determine sua velocidade angular quando θ = 90 ° .
A barra de 20k g é liberada do repouso quando θ = 0 ° . Determine a velocidade angular da barra quando θ = 90 ° . A mola tem um comprimento não deformada de 0,5m .