Enunciado
Mecânica e Resistência dos Materiais - Dinâmica: Mecânica para Engenharia - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 14.Problemas - Ex. 51
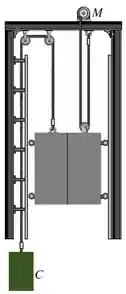
O elevador de carga e a carga têm massa total de 800 kg, e o contrapeso tem massa de 150 kg. Em um dado instante, o elevador tem uma velocidade para cima de 2 m/s e uma aceleração de 1,5 m/s2. Determine a potência gerada pelo motor neste instante se ele opera com uma eficiência de .
Passo 1
O enunciado nos dá as seguintes informações:
Massa total elevador de carga: ;
Massa contrapeso: kg;
Velocidade do elevador: m/s;
Aceleração do elevador: ;
Eficiência do motor: .
Devemos determinar a potência gerada pelo motor neste instante.
Vamos desenhar o diagrama de corpo livre da caixa e do elevador de carga, respectivamente:
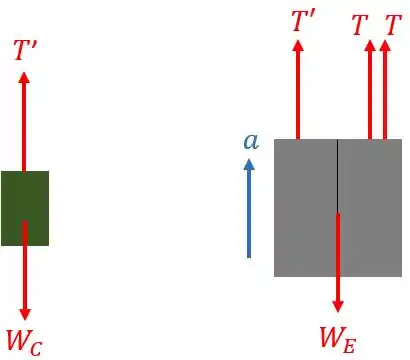
Onde e são a força peso do contrapeso e elevador, respectivamente; é a força de tração exercida pelo cabo que liga o elevador ao motor; e é a força de tensão exercida pelo cabo que liga o contrapeso ao elevador.
Como o contrapeso e o elevador estão ligados por um mesmo cabo, a velocidade e a aceleração de ambos terão o mesmo valor em módulo.
Passo 2
Primeiramente, vamos analisar os diagramas de corpo livre aplicando a Equação do Movimento:
Para o contrapeso, temos que
Para o elevador, temos que, no eixo
Substituindo o valor de , obtemos
Passo 3
A questão pede para determinarmos a potência do motor. Para isso, utilizaremos somente os dados da força de tensão , pois é ela que liga o elevador ao motor.
Sabemos que, por definição, a potência é dada por
Como podemos ver na imagem fornecida pelo enunciado e pelo diagrama de corpo livre do elevador, a força será igual à .
Logo, temos que
Esta é a potência de saída, ou seja, a potência necessária para conseguir movimentar o elevador nas condições dadas.
Devemos utilizar a eficiência do motor para obter a potência de entrada produzida por ele.
Sabemos que
Colocando em evidência, temos que