Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 2.Problemas - Ex. 125
Os cursores A e B são conectados por um fio de 635 mm de comprimento e podem deslizar livremente sobre as hastes sem atrito. Se uma força Q de 267 N é aplicada no cursor B, como mostrada na figura, determine a tração no fio quando , a intensidade da força P necessária para se manter o equilíbrio do sistema.
Passo 1
Alô Alô pessuar, belezinha??
Bora pra mais uma?
Primeiro passo e o nosso D.C.L
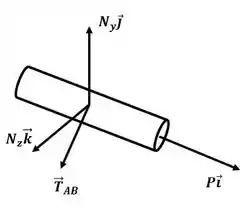
Passo 2
Agora iremos encontrar as coordenadas de posição dos pontos A e B.
Vamos encontrar a distância do ponto A ao ponto B
Agora iremos substituir por .
Vamos encontrar o valor de z usando o valor conhecido de magnitude AB
Vamos substituir por
Em seguida, vamos escrever o vetor posição de AB substituindo por na equação (1).
Passo 3
Nesse passo iremos encontrar o vetor unitário
Encontraremos o vetor força ou tensão no fio AB
Passo 4
- Vamos escrever o vetor do colar B,
- Vamos escrever o vetor força do colar A
O colar B terá reações ao longo da direção x e y, pois irá se mover livremente ao longo da direção z.
Vamos escrever o vetor força Q.
Aplicando a equação de equilíbrio de forças no ponto B.
Iguale os coeficientes a zero
Passo 5
O colar A terá reações ao longo da direção y e z, pois irá se mover livremente ao longo da direção x.
Escreveremos o vetor força P
Aplicando a equação de equilíbrio de forças no ponto A
Vamos igualar os coeficientes igual a 0.
Portanto, a magnitude da força P necessária para manter o equilíbrio é de .