Uma vista de topo de um carro está mostrada na figura. Duas diferentes posições, e , são consideradas para a colocação de um macaco. Em ambos os casos, todo o lado direito do carro é levantado do chão. Determine as forças de reação normais em e e a força vertical necessário do macaco, para cada uma das duas posições. Considere que o carro de é rígido. O centro de massa está na linha média do carro.
Passo 1
Quando o carro está prestes a se erguer do chão, podemos dizer que existe equilíbrio dos torques e das forças resultantes.
Vamos começar analisando o caso em que o macaco é colocado na posição . Precisamos definir alguns eixos para poder fazer as contas:
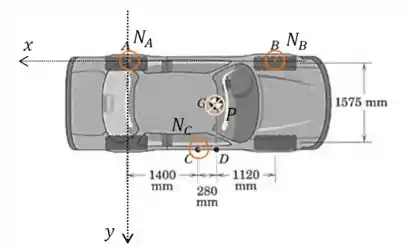
O símbolo representa uma força saindo do plano da página e o representa uma força entrando. Nesse caso o lado direito do carro está sendo levantado pelo ponto .
Passo 2
Olhando para a imagem, vamos encontrar expressões para os momentos em relação a cada um dos eixos.
Para temos que multiplicar cada força pela sua distância perpendicular até o eixo :
Dessa equação já podemos tirar o valor de :
E agora a mesma coisa para :
Se substituirmos o valor de que acabamos de achar já podemos calcular também:
E fica faltando só calcular , mas para isso vamos precisar de uma nova equação de equilíbrio.
Passo 3
Já consideramos o equilíbrio dos momentos, agora vamos considerar o equilíbrio das forças:
Lembre que as forças representadas no nosso desenho estão saindo/entrando do plano da página, então:
Substituindo os valores numéricos:
Beleza, então quando o macaco é colocado no ponto temos:
Agora vamos ver o que acontece quando colocamos no ponto .
Passo 4
Primeiro vamos refazer o desenho:
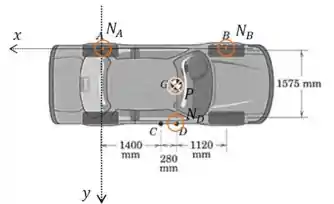
Perceba que não mudou praticamente nada, só trocamos a normal por em uma posição diferente.
Vamos escrever os momentos:
E já podemos resolver essa equação para encontrar :
Agora o momento em relação ao eixo :
E podemos substituir o valor de para calcular :
E agora vamos usar o equilíbrio das forças para calcular a variável que falta (
E então no caso em que o macaco é colocado no ponto temos:
Resposta
Quando o macaco é colocado no ponto : , e . Quando é colocado no ponto : , e .