Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 69
Uma banqueta de três pernas está submetida à carga , como mostrado. Determine a força de reaçõa vertical sob cada perna. Despreze o peso da banqueta.
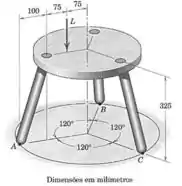
Passo 1
Vamos começar definindo alguns eixos e desenhando as forças que atuam sobre a banqueta:
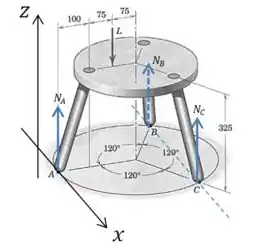
Como as duas forças e são perfeitamente simétricas (inclusive em relação à força ), podemos garantir que:
Passo 2
Agora vamos usar alguma equação de equilíbrio que seja convienente. Se calcularmos o momento resultante em relação ao eixo , por exemplo, ao menos uma das variáveis desconhecidas vai sumir da equação:
Então vamos multiplicar cada força pela sua distância perpendicular até o eixo :
E esse ângulo de é calculado considerado que a linha que pasa pelo ponto divide o ângulo de ao meio:
Então:
Passo 3
Para encontrar a força vamos usar o equilíbrio das forças na direção do eixo :
Resposta
As forças nas pernas da banqueta são e .