Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 3.4 - Ex. 65
A parte de um lustre que é sustentada por correntes tem a forma de uma parte de casca esférica. Se a massa da parte de vidro é , determina a força trativa em cada uma das correntes.
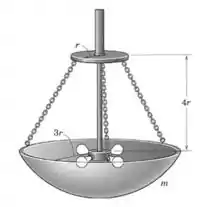
Passo 1
Como as correntes estão distribuídas de forma simétrica, a tensão nas três tem que ser igual:
Como só temos uma variável desconhecida, também só precisamos de uma equação de equilíbrio para resolver o problema! Vamos usar então a seguinte equação:
Ou seja, a resultante das forças na direção vertical é nula.
Passo 2
Precisamos projetar a força na direção do eixo , e para isso precisamos definir um ângulo:
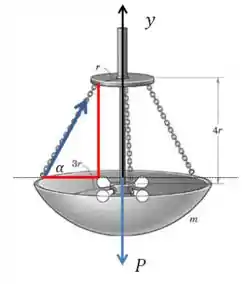
E como temos três forças atuando no mesmo sentido do eixo :
Agora só falta calcular o ângulo (dê uma olhada no nosso desenho):
E substituindo isso na expressão:
Resposta
A força trativa em cada corrente é .