Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 12.Problemas - Ex. 51

A curva em um circuito de velocidade tem raio de 300 m e velocidade de segurança de 192 km/h. (Ver no Problema Resolvido 12.5 para a definição da velocidade de segurança.) Sabendo que o carro de corrida começa a derrapar na curva quando viaja a uma velocidade de 288 km/h, determine (a) o ângulo de inclinação θ , (b) o coeficiente de atrito estático entre os pneus e a estrada sob as condições prevalentes, (c) a velocidade escalar mínima para a qual o mesmo carro poderia fazer a curva.

Passo 1

Borá lá gurizada, o enunciado pede que a gente determine o ângulo de inclinação θ , (b) o coeficiente de atrito estático entre os pneus e a estrada sob as condições prevalentes, (c) a velocidade escalar mínima para a qual o mesmo carro poderia fazer a curva, então segura na minha mão e vem começando a esboçar um diagrama de forças :D

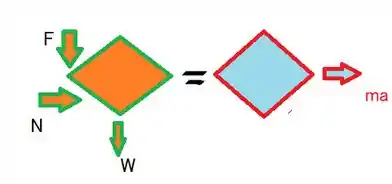
Sabendo que o peso é dado por:

W = m g

E a Aceleração

a = v 2 ρ

Passo 2

Fazendo o somatório das forças do esboço anterior em x e y temos respectivamente:

Σ F x = m a x :         F + W sin ⁡ θ = m a cos ⁡ θ

F = m v 2 ρ cos ⁡ θ - m g sin ⁡ θ

Σ F y = m a y :         N - W cos ⁡ θ = m a sin ⁡ θ

N = m v 2 ρ sin ⁡ θ + m g cos ⁡ θ

Passo 3

  1. Ângulo de inclinação: Velocidade nominal v = 192 km/h = 53,33 m / s. F = 0 na velocidade nominal.

    2. 0 = m v 2 ρ cos ⁡ θ - m g sin ⁡ θ

    tan ⁡ θ = v 2 ρ g = ( 53,33 ) 2 300 10 = 0.96199

    θ = 43 . 47 °

    Passo 4

  2. a derrapar na curva.

    3. v = 288   k m /h = 80   m /s

    F = μ N         μ = F N = v 2 cos ⁡ θ - ρ g sin ⁡ θ v 2 sin ⁡ θ - ρ g cos ⁡ θ

    Substituindo os valores temos:

    μ = ( 80 ) 2 cos ⁡ 43 . 47 ° - 1000 10 sin ⁡ 43.47 ° ( 80 ) 2 sin ⁡ 43 . 47 ° + 1000 10 cos ⁡ 43.47 ° = 0.39009

    Passo 3

  3. Velocidade mínima.

F = - μ N

- μ = v 2 cos ⁡ θ - ρ g sin ⁡ θ v 2 sin ⁡ θ - ρ g cos ⁡ θ

v 2 = ρ g sin ⁡ θ - μ cos ⁡ θ cos ⁡ θ + μ sin ⁡ θ

Substituindo os valores:

= 1000 10 sin ⁡ 43.47 ° - 0.39009 cos ⁡ 43.47 ° cos ⁡ 43 + 89 ° + 0.39009 sin ⁡ 51.875 °

v = 126   k m / h

Resposta

a )   θ = 43 . 47 °

b )   μ = 0.390

c )   v = 126   k m / h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

131. O avião a jato de 12Mg tem uma velocidade constante de 950 km/h ao voar ao longo de uma linha reta horizontal. O ar penetra nas cavidades de entrada de ar S a uma taxa de 50 m 3 s . Se o motor qu
128. O recipiente deposita cascalho sobre a correia transportadore a uma taxa de 750 kg/min. Se a velocidade da correia é 1,5m/s, determine o quanto a tração na porção superior da correia deve ser mai
132. O carrinho tem massa M e está cheio de água que tem massa m 0 . Se uma bomba ejeta água por um bocal que tem uma área transversal A, a uma taxa constante de v 0 em relação ao carrinho, determine
129. O trator com o tanque vazio tem massa total de 4Mg. O tanque fica cheio com 2 Mg de água. A água é descartada a uma taxa constante de 50 kg/s, a uma velocidade constante de 5m/s, medida em relaçã
140. Determine a intensidade da força F como uma função do tempo, que dever ser aplicada à extremidade da corda em A para levantar o gancho H com uma velocidade constante v = 0,4 m s . Inicialmente, a