Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.6 - Ex. 157

Um mecanismo de avanço intermitente para fita perfurada F consiste no elemento DAB acionado pela manivela OB. O traçado do movimento do dente D é indicado pela linha tracejada. Determine o módulo da aceleração de D no instante representado quando ambos OB e CA estão horizontais se OB possui uma velocidade de rotação constante no sentido horário de 120 rpm.

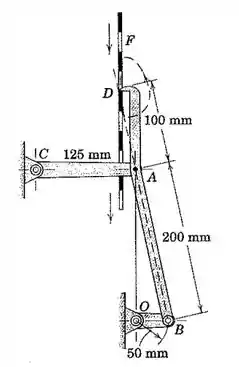
Passo 1

Galera, esta figura está muito confusa, então primeiro vamos organizar todos os dados do enunciado e fazer um esboço do que realmente importa no mecanismo. Importante enxergar o traçado do movimento de D.

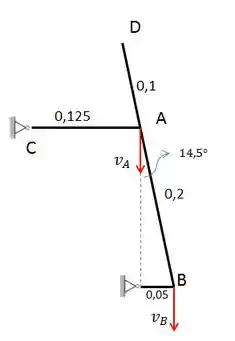
Pronto! Agora vamos começar o desenvolvimento calculando a velocidade de B.

v B = ω B O × r B O = - 120 r p m × 2 π 60 k ^ × 0,05 i ^ = - 0,2 π j ^   m / s

Como A e B são paralelas, então:

v A = v B = - 0,2 π j ^   m / s

ω A B = 0

Podemos também calcular a velocidade da barra AC:

ω A C = v A r A / C = - 0,2 π 0,125 = - 5,03   k ^   r a d / s

O ângulo identificado na figura foi encontrado através do seno do triangulo OAB:

α = s e n - 1 0,05 0,2 = 14,5 °

Passo 2

Vamos começar a calcular as acelerações.

O ponto B possui apenas aceleração normal, portanto:

a B = a B n = - r B O ω B O 2 =   -   0,05 4 π 2 = - 7,90   i ^   m / s 2

A aceleração de A pode ser representada a partir da barra AC por:

a A = - r A C ω A C 2 + α A C × r A C = - 0,125 - 5,03 2 i ^ + α A C k ^ 0,125 i ^

a A = - 3,16 i ^ + 0,125 α A C   j ^

Agora, vamos usar a equação da aceleração relativa para os pontos A e B.

a B = a A + a B / A n + a B / A t

Onde:

a B / A n = ω × ω × r B / A = 0

a B / A t = α × r B / A = α A B 0,194 i ^ + 0,05 j ^ m / s 2

Agora, vamos substituir os valores encontrados na equação da aceleração relativa:

- 7,90   i ^ = - 3,16 i ^ + 0,125 α A C   j ^ + α A B 0,194 i ^ + 0,05 j ^

Decompondo nas direções, temos o sistema:

- 7,90   i ^ = - 3,16 i ^ + α A B 0,194 i ^

0 = 0,125 α A C   j ^ + α A B 0,05 j ^

Resolvendo o sistema, temos:

α A B = - 24,43 k ^   r a d / s 2

α A C = 9,77 k ^   r a d / s 2

Passo 3

Agora, vamos repetir o passo anterior, mas fazendo a aceleração relativa de C e B.

a D = a B + a D / B n + a D / B t

Onde:

a D / B n = ω × ω × r D / B = 0

a D / B t = α A B × r D / B = - 24,43 k ^ × - 0,3 s e n 14,5 i ^ + 0,3 c o s 14,5 j ^ = 7,1 i ^ + 1 , 8 j ^ m / s 2

Agora, vamos substituir os valores encontrados na equação da aceleração relativa:

a D = - 7,90 i ^ + 7,1 i ^ + 1,83 j ^ = - 0,8 i ^ + 1 , 8 j ^   m / s 2

Como é pedido o módulo da aceleração de D:

a D = ( - 0,8 ) 2 + 1,8 2 = 1,997   m / s 2

Resposta

a D = 1,997 m s 2 o u   1997 m m s 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O raio do pino B fixo à manivela AB desliza livremente ao longo da ranhura no membro CDE. Se AB gira com o movimento mostrado, determine a velocidade angular de CDE no instante mostrado.
A lança telescópica do guindaste gira com a velocidade angular e a aceleração angular mostradas. No mesmo instante, a lança está se estendendo com uma velocidade constante de 0,15 m/s, medida em relaç
No instante θ = 45 ° , o membro DC tem uma velocidade angular ω D C = 4r a d / s e uma aceleração angular α D C = 2r a d / s 2 . Determine a velocidade angular e a aceleração angular da barra AB nesse
No instante mostrado, a barra AB tem uma velocidade angular ω A B = 4r a d / s e uma aceleração angular α A B = 2r a d / s 2 . Determine a velocidade angular e a aceleração angular da barra CD nesse i
Em um dado instante, a barra AB tem os movimentos angulares mostrados. Determine a velocidade angular e a aceleração angular da barra CD nesse instante. Há um anel em C.