Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 99
O vaso de pressão cilíndrico tem raio interno de e espessura de parede de . É feito de chapas de aço soldadas ao longo de uma linha de junção a em relação à horizontal. Determine as componentes de tensão normal e da tensão de cisalhamento ao longo dessa linha de junção, se o vaso estiver sujeito a uma pressão interna de .
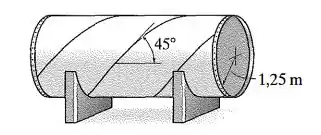
Passo 1
Fala aí pessoal, vamos para mais um exercício de resmat. A primeira coisa que precisamos fazer para desenhar um círculo de mohr é um estado de tensões bem definido. Temos que as tensões em e são:
Logo:
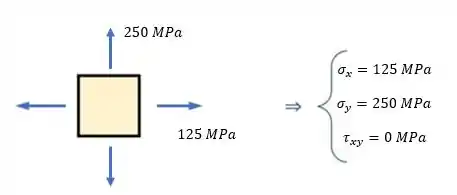
Passo 2
Em seguida, temos que determinar o centro do círculo, definido como:
O segundo ponto que vamos determinar representa as tensões no eixo do seu estado de tensões e é definido como:
O próximo ponto é determinar o raio do círculo de Morh, que será
Passo 3
Na junção, temos:
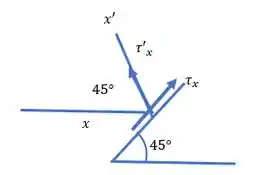
Com isso, temos: