Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 8.Problemas - Ex. 111
111. Resolva o problema , considerando que o tambor está girando em sentido anti-horário
Passo 1
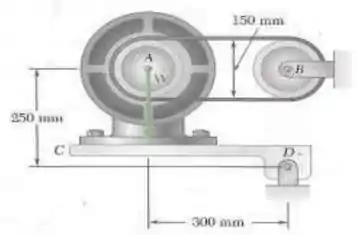
Bom! Vamos lá para mais um probleminha sobre correias. Sendo assim, qual é a primeira coisa que temos que fazer?
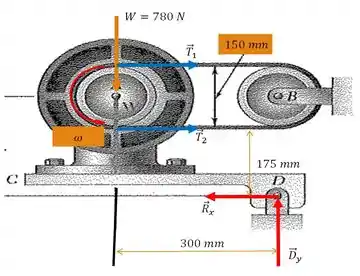
Ora bolas! Já tá meio que repetitivo, mas é o procedimento padrão; tá? Temos que fazer o diagrama de corpo livre para o nossos sisteminha. Vamols lá! Façamos primeiro, o diagrama para o motor pivotante, indo para o ponto :
Passo 2
E agora que já fizemos o diagrama de corpo livre, bora utilizar a velha relação que conhecemos para o atrito em correias na condição iminente de deslizamento. Só que como o tambor gira em sentido anti-horário e estamos aproveitando a figura da questão anterior, brincadeiras a parte, dessa vez devemos usar uma convenção diferente, a seguir:
Onde , dessa vez, vai ser a tração máxima e vai ser a tração mínima. E como a questão já nos fornece o valor de , igual a . E o ângulo , que é o ângulo subentendido pelo arco do tambor sobre a qual a correia está enrolada, ao olhar a figura percebemos que vale ou radianos. Sendo assim, obtemos que:
Passo 3
a) E ao olhar a figura novamente:
Vemos que a próxima coisa que temos que fazer, é simplesmente aplicar o somatório dos momentos em relação ao ponto:
E o valor de é dado por:
Passo 4
b) Em seguida, como a questão nos pede para determinar o maior torque que pode ser transmitido ao tambor quando o tambor acionador está girando em sentido horário, vamos começar a resolução desse item seguindo a velha cartilha. Por isso, façamos o diagrama de corpo livre para o tambor :
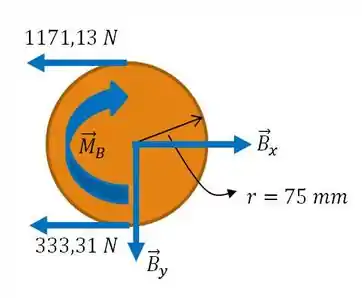
E para achar o torque no tambor em , basta fazer o somatório dos momentos em relação ao momento :
Como encontramos um valor positivo, significa que nossa convenção adotada foi correta, e o torque no tambor realmente ocorre no sentido horário.
Pronto! Encontramos nossas respostas.
Resposta
a)
b)