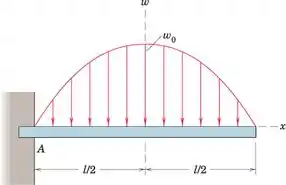
Derive expressões para o cortante V e o momento M em termos de x para a viga em balanço de Prob. 5/114 mostrado novamente aqui. O carregamento é parabólico.
Passo 1
A seguir, como a extremidade B está livre (a da extremidade direita), cortaremos o ponto na distância 1/2 x do ponto B e analisaremos a porção da viga à direita.
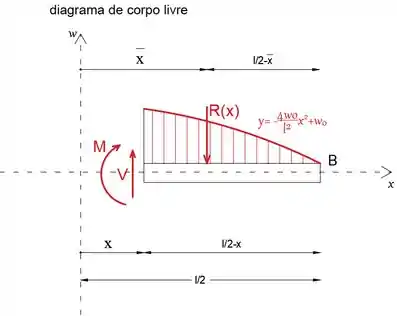
Ao igualar a soma das forças na direção y a zero, derivaremos a expressão da força de cisalhamento na viga.
Ao igualar a soma dos momentos a zero, derivaremos a expressão para o momento fletor na viga
Passo 2
Observe que, como R(x) = V expressão (1), podemos escrever a expressão acima como:
Observe que tanto M quanto V são expressos como função de R(x), então teremos que determinar a intensidade da resultante. Para fazer isso, precisaremos escrever a função da parábola.
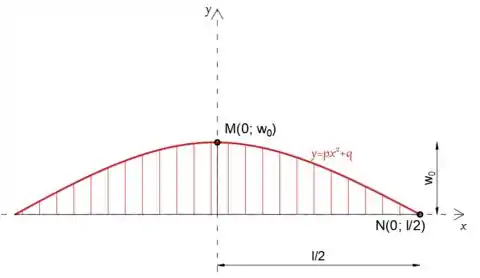
Função parabólica:
Vamos colocar as coordenadas do ponto M na equação
Passo 3
Agora vamos colocar as coordenadas do ponto B na equação
Substitua q por w0
Uma vez que determinamos os coeficientes p e q, podemos escrever a função parabólica
Passo 4
Determinaremos o R resultante integrando a função parabólica no intervalo:
Substitua x por l/2 e x
Passo 5
E a posição da resultante é:
Substitua x por l/2, x
Passo 6
Observe que a resultante é igual à área sob a função ol parábola, então vamos dividir a área em áreas infinitesimais no intervalo ,
A área total da figura sombreada, ou seja, a resultante da carga distribuída é:
Como a área é simétrica em relação ao eixo y, podemos escrever a expressão acima como
Integre o lado direito da equação em relação ao dy
Passo 7
Em seguida, substituiremos y por
Agora vamos integrar o lado direito da equação em relação a dx
Substitua x por
Finalmente, concluímos que a área total é:
Passo 8
Para determinar a expressão do momento fletor na viga, substituiremos R(x) e pelas expressões (3) e (4) na expressão (2)
Substitua R(x) pela expressão (1)
A expressão final para o momento fletor é: