Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 158
Um rebocador motorizado reboca uma barcaça com um cabo que tem uma massa de 14 kg por metro de comprimento. Observa-se que a tangente ao cabo no ponto A é horizontal. Determine as tensões em A e B.
Passo 1
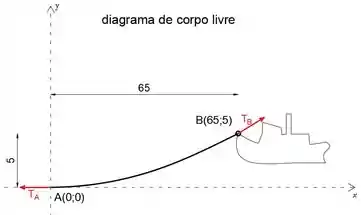
Primeiro, vamos desenhar o diagrama de corpo livre do cabo.
Observe que, uma vez que o cabo suporta apenas seu peso, o cabo tem uma forma conhecida como catenária
Como o cabo é horizontal em A, podemos dizer que o ponto A é o início do sistema de coordenadas da função do cabo, então a tensão em A é:
Passo 2
O peso por metro de comprimento é igual à massa por comprimento vezes a gravidade:
Observe que a função do cabo é:
Substitua m por seus valores e coloque as coordenadas do ponto B na equação
Passo 3
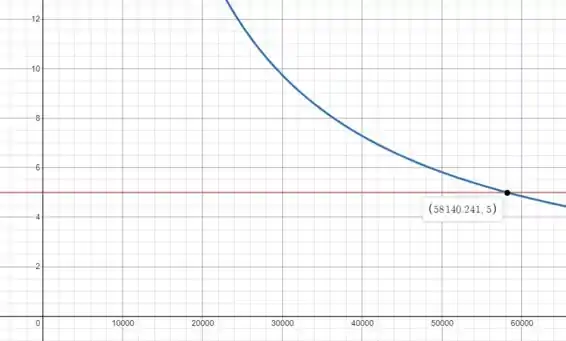
Usando uma calculadora gráfica como o Desmos (link nos comentários), vamos representar graficamente a função e e ler a solução do ponto de intersecção
Agora podemos calcular m da expressão (1)
A seguir, usando a expressão (5/22), podemos determinar a tensão em B.
Substitua yB, T0 e por seus valores.