Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 58
Localize o centroide da área composta.
Passo 1
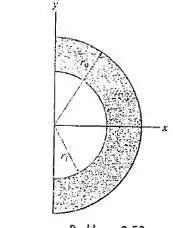
Cara, queremos o centroide dessa figura.
Uma coisa importante é que a figura é simétrica em relação a , então a gente já pode dizer que a coordenada do centroide é zero, e focar só em achar a coordenada .
Então, galerinha, pega o bizu! Nessas questões que envolvem buracos, a gente vai fazer o seguinte: procede normalmente! A única coisa que vai mudar é que o buraco vai entrar na conta como se tivesse área negativa! Até que faz sentido, né? Show!
Vamos usar nossa fórmulinha
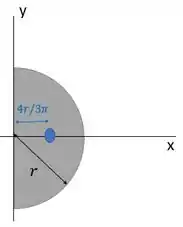
Aqui a gente vai ter que usar também que o centro de massa de um semi circulo está a uma distância , como já vimos na teoria.
Passo 2
Temos dois semicírculos. O maior de e menos
Para o maior, a área vai ser
E a coordenada do centroide vai distar da origem
Para o círculo menor, vamos dizer que área é negativa, porque na verdade ele é um buraco na nossa seção, então fica
E a coordenada do centroide fica parecida, só muda que :
Passo 3
Então vai ficar assim na formula do centroide:
Cortando o que tem que cortar e dando uma boa arrumada na casa, vamos chegar no nosso resultado final: