Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 9.Problemas - Ex. 49
Localize o centroide do fio. Se o fio for suspenso por , determine o ângulo que o segmento faz com a vertical quando o fio está em equilíbrio.
Passo 1
A chave dessa questão é entender essa questão é ver o que tem que acontecer para o fio ficar em equilíbrio quando fica pendurado. Mas primeiro vamos olhar para a primeira parte do problema, achar o centroide do fio.
Para a parte horizontal do fio, o centro de massa dela é na origem do sistema, porque ela está no eixo , então , e está simétrica em relação ao eixo , então . Beleza, vamos olhar para a outra parte então!
O comprimento da parte a gente tira da trigonometria do problema!
Então o centro de massa de está na posição:
Passo 2
Então podemos ir para a fórmula do centroide!
Passo 3
O que vai acontecer quando o fio for suspenso é que tem que ter equilíbrio de momentos em relação ao centro de massa, senão o fio vai rodar. Pra isso, a tração tem que passar pelo centro de massa. Então, se é o centro de massa, o fio vai ficar suspenso em equilíbrio quando for vertical, já que a tração é vertical!
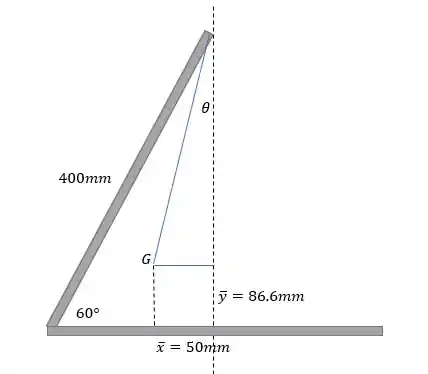
Da trigonometria, vamos calcular o :
Com o auxílio da calculadora, descobrimos !
Então o ângulo que faz com a vertical é o complementar para , que é o ângulo original do fio com a vertical.