Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 141
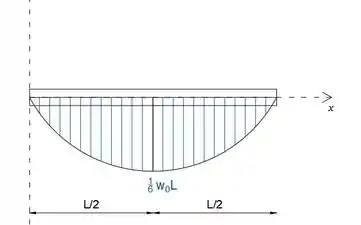
Desenhe os diagramas de cisalhamento e momento para a viga simples carregada linearmente mostrada. Determine a magnitude máxima do momento fletor M.
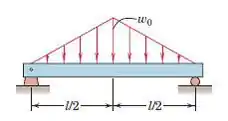
Passo 1
Primeiro, vamos determinar as forças de reação do diagrama de corpo livre usando as equações de equilíbrio
Observe que substituímos as cargas distribuídas por suas resultantes
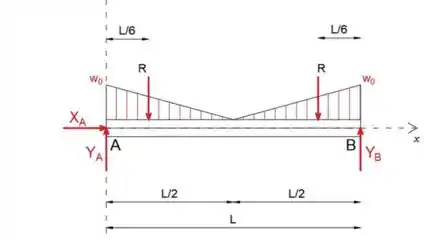
Passo 2
A partir daqui, podemos construir o diagrama de força cortante
Usando a fórmula , calcularemos as forças de cisalhamento da esquerda para a direita
Observe que o diagrama de força cortante é uma curva, por causa da carga distribuída triangular, também tem dois "saltos" positivos em A e B devido às reações de apoio
A inclinação do diagrama diminui ao longo do intervalo m, uma vez que a carga distribuída diminui ao longo do mesmo intervalo, enquanto aumenta ao longo do intervalo [L / 2≤x≤L] m, uma vez que a carga distribuída aumenta na mesma faixa
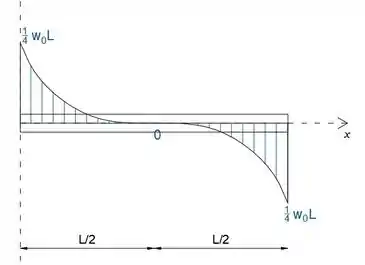
Passo 3
A seguir, usaremos o diagrama de força cortante para construir o diagrama de momento fletor
Uma vez que o diagrama de força cortante é uma curva, não podemos usar a expressão [Mx= , mas sabemos que o momento é igual a zero nas extremidades A e B, e que é máximo em x = L / 2 m (quando o cisalhamento é igual a zero), então usaremos isso para construir o diagrama
Observe que a inclinação para o diagrama de momento está diminuindo ao longo do intervalo [0≤x≤L / 2] e aumenta ao longo do intervalo [L / 2≤x≤L], uma vez que a força de cisalhamento diminui ao longo do intervalo [0≤x≤ L / 2] e aumenta ao longo do intervalo [L / 2≤x≤L]
Conforme calculado acima, o momento fletor máximo é:
