Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 75
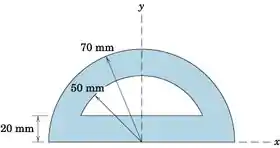
Determine a coordenada y do centróide da área sombreada. (Dica: consulte a solução do Problema 5/41.)
Passo 1
Lembre-se da teoria de que as coordenadas do centroide de um objeto podem ser encontradas usando a (s) equação (ões):
No entanto, no caso de densidade constante e um objeto bidimensional, podemos escrever a massa como:
Passo 2
A partir daqui, as equações se tornam
Fazendo isso para todas as equações
Passo 3
Tenha muito cuidado com a localização do eixo. Eu não posso enfatizar isso o suficiente. Lembre-se de que tudo o que fazemos e o resultado será em relação a esse eixo. Tenha isso em mente e esses problemas se tornam muito mais simples
Aqui, separamos o problema em 2 partes, conforme mostrado na figura. Começaremos com a parte 1, que é a mais fácil. Usando o problema de amostra 5/2 de massa. Uma vez que temos uma figura bidimensional e a densidade é uniforme, estamos apenas interessados na área (ignore a densidade porque ela cancela o que significa que encontramos apenas a área).
Em seguida, temos uma figura circular aqui, temos que usar os resultados do Problema 5/41 conforme sugerido. O resultado desse problema foi:
Passo 4
No nosso caso h = 20 mm e a = 50 mm, portanto (este é um orifício, portanto temos massa negativa):
E:
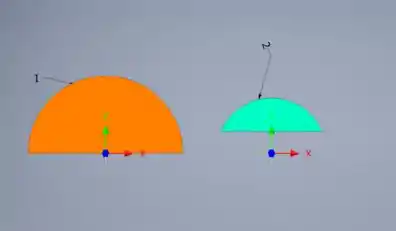
Passo 5
Temos todas as informações de que precisamos para chegar a uma conclusão, então escrevemos:
Resposta
Separe as figuras em 2 e, em seguida, observe a solução do Problema 5/41. Certifique-se de usar grad ao calcular as funções trisonométricas!