Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 152

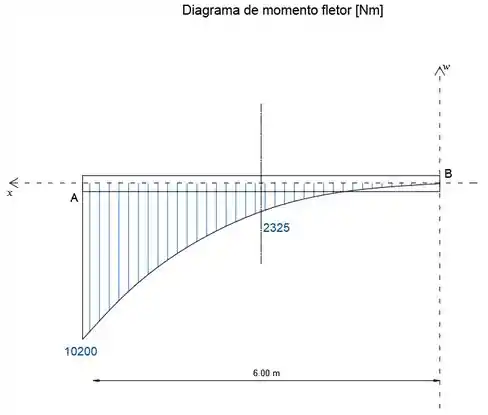
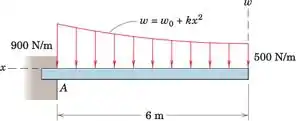
Desenhe os diagramas de cortante e momento para a viga de Prob. 5/116 repetido aqui e especifique o cisalhamento V e o momento M no comprimento médio da viga.

Passo 1

A primeira coisa que precisamos fazer é determinar os coeficientes da função de carregamento

Função de carga:

w = w 0 + k x 2

Podemos notar que existem dois coeficientes desconhecidos, então precisaremos escrever duas equações para determiná-los

Em x = 0, a intensidade é w = 500, então colocaremos esses valores na função

500 = w 0 + k ∙ 0 2                     ⇒                     w 0 = 500

Em x = 6, a intensidade é w = 900, então colocaremos esses valores na função

900 = w 0 + 6 2

Substitua w0 por 500

900 = 500 + k ∙ 6 2                     ⇒                     k = 900 - 500 6 2 = 11.111

Como determinamos os coeficientes w0 e k, podemos escrever a função de carregamento como:

w = 500 + 11.111 x 2

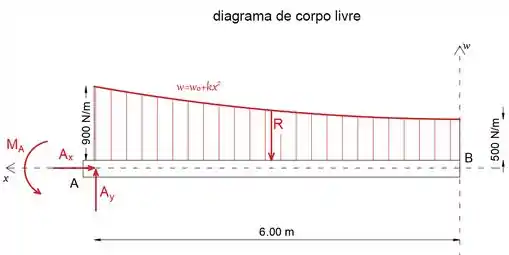
Passo 2

A seguir, vamos cortar e analisar a parte do feixe ao longo do intervalo 0 ≤ x ≤ x

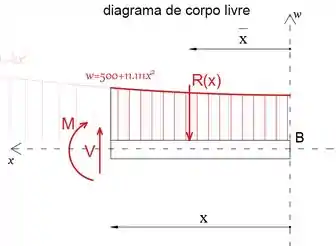
Determinaremos o R resultante integrando a função parabólica no intervalo: 0 ≤ x ≤ x

R x = ∫ 0 x 500 + 11.111 x 2   d x

R x = 500 x + 11.111 x 3 3 0 x

Passo 3

Substitua x por x

R x = 500 ∙ x + 11.111   x 3 3

R x = 3.704 x 3 + 500 x                     ( 1 )

E a distância do eixo w é

x - = 1 R x ∫ 0 x x 500 + 11.111 x 2   d x

x - = 1 R x ∫ 0 x 500 x + 11.111 x 3   d x

x - = 1 R x ∫ 0 x 500 x 2 2 + 11.111 x 4 4 0 x

Passo 4

Substitua x por 6 e R(x) por 3,704x3 + 500x

x - = 1 3.704 x 3 + 500 x 500 ∙ x 2 2 + 11.111 ∙ x 4 4

x - = 2.778 x 4 + 250 x 2 3.704 x 3 + 500 x                     ( 2 )

Ao igualar a soma das forças na direção y a zero, derivaremos a expressão da força de cisalhamento na viga.

∑ F y = 0

V - R x = 0

V = R x

Substitua R(x) pela expressão (1)

V = 3.704 x 3 + 500 x

A fim de determinar a força de cisalhamento no ponto médio da viga, substituiremos x por 3

V x = 3 = 3.704 ∙ 3 3 + 500 ∙ 3

V x = 3 = 1600   N

Ao igualar a soma dos momentos a zero, derivaremos a expressão para o momento fletor na viga

∑ M = 0

M + V ∙ x - R x ∙ x - = 0

M = R x ∙ x - - V ∙ x

Passo 5

Observe que, como R(x) = V (da etapa 4), podemos escrever a expressão acima como:

M = R x x - - x

Substitua R(x) e x - pelas expressões (1) e (2)

M = 3.704 x 3 + 500 x 2.778 x 4 + 250 x 2 3.704 x 3 + 500 x - x

M = 3.704 x 3 + 500 x 2.778 x 4 + 250 x 2 3.704 x 3 + 500 x - 3.704 x 4 - 500 x 2 3.704 x 3 + 500 x

M = 3.704 x 3 + 500 x - 0.926 x 4 - 250 x 2 3.704 x 3 + 500 x

M = - 0.926 x 4 - 250 x 2

A fim de determinar o momento fletor no ponto médio da viga, vamos substituir x por 3

M x = 3 = - 0.926 ∙ 3 4 - 250 ∙ 3 2

M x = 3 = - 2   325   Nm

Passo 6

Trace a função da força de cisalhamento para obter o diagrama da força de cisalhamento.

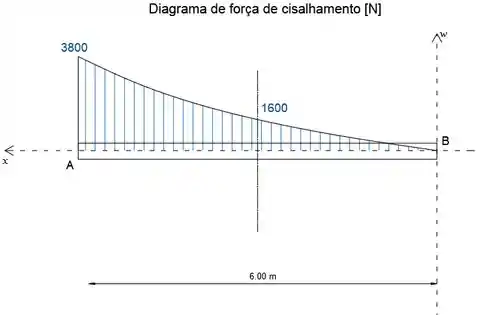
Trace a função do momento fletor para obter o diagrama do momento fletor.

Resposta

V x = 3 = 1600   N

M x = 3 = - 2   325   Nm

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Por que os valores numéricos das magnitudes das grandezas físicas são meramente convencionais? O que são grandezas de base em um sistema de unidades? Por que distintos sistemas coerentes podem ter dif
Qual é a diferença entre dimensão de uma grandeza física e unidade dessa grandeza? Por que são estabelecidas unidades de base e unidades derivadas? E o que é uma grandeza física adimensional? Exemplif
Como explicar a relação entre as unidades de força no sistema Internacional e no Sistema Técnico? Idem quanto às unidades de massa nesses sistemas
Qual é a diferença entre a notação científica e a notação de engenharia, ao escrever valores numéricos? Qual é a vantagem de cada uma dessas notações?
Qual é a diferença entre grandeza escalar e grandeza vetorial? Quais são as diferenças entre vetor livre, vetor deslizante e vetor fixo? Como exemplificar?