Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 3.Problemas - Ex. 57b
Desenvolver uma expressão aproximada para o ângulo de torção de um eixo, de forma de tronco de cone no Prob 3.56, substituindo o tronco de cone por n eixos cilíndricos de iguais comprimentos e raios onde . Qual é a resposta do Prob. 3.56 e a porcentagem de erro nesta resposta, se a expressão obtida for usada com (a) n=4, (b) n=8 (c) n=20; (d) n=100
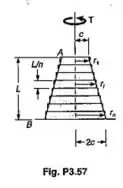
Passo 1
Vamos fazer o mesmo processo da questão anterior, mas com
Então:
Agora vamos calcular diferentes alturas:
E agora calculamos a Soma de Riemman:
Passo 2
E aplicamos a soma na equação do ângulo de torção:
Logo:
Passo 3
A resposta analítica é:
E nós encontramos:
Se dividirmos um pelo outro encontraremos o erro e subtraindo 1
Resposta
Exercícios de Livros Relacionados
(a) Para o eixo de alumínio mostrado G = 27G P a , determine o torque T 0 que provoca um ângulo de torção de 2° e (b) o ângulo de torção provocado pelo mesmo torque T 0 em um eixo cilíndrico cheio de
A barra de alumínio A B G = 27G P a está ligada a barra de latão B D G = 39G P a . Sabendo que a parte CD da barra de latão é vazada e tem um diâmetro interno de 40 mm, determine o ângulo de torção em
No Problema 3.114, determine o ângulo de torção permanente da barra.
Dois eixos de seção transversal cheia, cada um com 30 mm de diâmetro, são conectados pelas engrenagens mostradas. Sabendo que G=77,2 GPa, determine o ângulo que extremidade em A descreve quando um tor
Uma barra de aço é usinada até a forma mostrada na figura, para obter um eixo cônico de seção transversal cheia ao qual são aplicados torque de intensidade T = 8473k N ⋅ m m . Considerado que o aço se