Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 3.Problemas - Ex. 100
O manipulador deuma esmeriladora industrial em miniatura pesa 2,7 N e seu centro de gravidade está sobre o eixo . O cabeçote do manipulador fica recuado no plano de modo que a linha BC forma um ângulo de com a direção . Mostre que o peso do manipulador e os dois binários e podem ser substituídos por uma força única equivalente. Além disso, considerando que e , determine a intensidade e a direção da força equivalente, o ponto em que sua linha de ação intercepta o plano .
Passo 1
Vamos começar o exercício desenhando o sistema equivalente na origem:
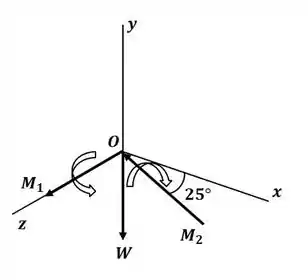
Dessa forma, o momento resultante será:
Percebemos que o momento resultante não possui componente na direção , e como a única força no sistema é o peso, que está agindo na direção , então esse sistema pode ser substituído por uma força de mesma magnitude e sentido que o peso, dessa forma:
Passo 2
Agora, para encontrar a localização do ponto que intercepta o plano , precisamos adotar um ponto no plano:
Dessa forma, o vetor que liga esse ponto à origem é dado por:
Sabemos que o momento resultante pode ser escrito através da equação:
Substituindo os valores conhecidos, temos:
Passo 3
Agora igualando as componentes e obtidas na última equação do passo 2, temos: