Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 5.3 - Ex. 38
A lança está sendo elevada pelo arranjo de cabo e polia mostrado. Se o ponto no cabo recebe uma velocidade constante , determine a velocidade angular e a aceleração angular da lança para .
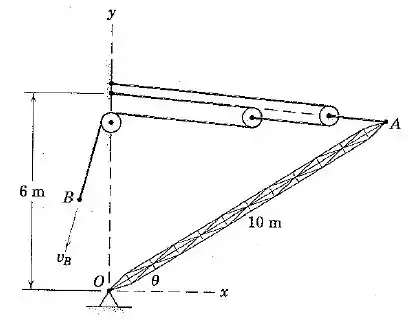
Passo 1
Vamos chamar de a distância entre o ponto e aquele ponto fixado na altura de .
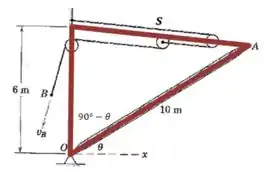
Perceba que a corda do ponto está ligada ao ponto por uma polia fixa e duas móveis. A polia fixa simplesmente transmite o movimento, mas nós sabemos que cada uma das duas polias móveis “divide o deslocamente por dois”:
E podemos dividir tudo por para encontrar:
E a velocidade é o negativo da derivada temporal do comprimento :
Mas nosso objetivo é encontrar e , então precisamos procurar mais relações.
Passo 2
Olhando para o triângulo que desenhamos, vamos aplicar a lei dos cossenos:
E agora podemos derivar em relação ao tempo:
E derivando pela segunda vez:
Mas como a velocidade é constante, podemos garantir que .
Agora podemos substituir para encontrar os valores.
Passo 3
Vamos usar , , então a velocidade angular é:
E agora para a aceleração angular:
Resposta
A velocidade angular é e a aceleração angular é .