Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 11.Problemas - Ex. 160

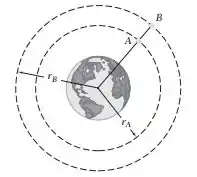
Dois satélites A e B percorrerem órbitas circulares coplanares em torno da Terra com altitudes de 190 e 320 km, respectivamente. Se em t = 0 os satélites estão alinhados como mostrado na figura e sabendo que o raio da Terra é R = 6.370 km, determine quando os satélites estarão radialmente alinhados de novo. (Veja as informações fornecidas nos Problemas 11.153-11.155.)

Passo 1

Vamos lá resolver mais essa. Vamos lembrar que a aceleração normal de um corpo em orbita é:

a n = g R 2 r 2

E também é definida como:

a n = v 2 r

Onde R é o raio da Terra e r é raio da órbita do corpo. Igualando as duas equações:

g R 2 r 2 = v 2 r → v = R g r

Onde

r = R + h

A circunferência da órbita tem o comprimento de s = 2 π r . Assumindo que os satélites tem velocidades constantes, logo s = v t . Assim,

2 π r = R g r T

T = 2 π R r 3 2 g = 2 π R R + h 3 2 g  

Como h B > h A , temos T B > T A , onde T A e T B são os períodos para os satélites completarem uma volta.

Passo 2

Agora, vamos assumir que T C seja o instante relacionado a próxima vez que os satélites estarão alinhados. Dessa forma, se no instante T C o satélite B completa N órbitas, o satélite A deve completar N+1 órbitas. Logo,

T C = N T B = N + 1 T A

N 2 π R R + h B 3 2 g = ( N + 1 ) 2 π R R + h A 3 2 g  

N = R + h A 3 2 R + h B 3 2 - R + h A 3 2 = 1 R + h B R + h A 3 2 - 1

N = 1 6370 + 320 6370 + 190 3 2 - 1 = 33,476   ó r b i t a s

Passo 3

Substituindo para B:

T C = N T B = N 2 π R R + h B 3 2 g

T C = 33,476 2 π 6370 6370 + 320 3 2 9,81 1 3600

T C = 51,2   h

Resposta

51,2 h

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O motorista de um automóvel diminui sua velocidade escalar numa taxa constante de 72 km/h para 48 km/h em uma distância de 225 m ao longo de uma curva de raio 450 m. Determine a intensidade da acelera
Um elevador de carga subindo com velocidade constante de 1,8 m/s passa por um elevador de passageiros que está parado. Quatro segundos depois, o elevador de passageiros começa a subir com uma aceleraç
A aceleração de uma partícula é definida pela relação a = - 60 x - 1,5 , onde a e x são expressos em m/s2 e metros, respectivamente. Sabendo que a partícula parte sem velocidade inicial em x 4 m, dete
Um projétil entra em um meio resistente em x = 0 com uma velocidade inicial v0 = 270 m/s e percorre 100 mm antes de entrar em repouso. Considerando que a velocidade do projétil é definida pela relação
O movimento de uma partícula é definido pela relação x = 2t3 - 15t2 + 24t + 4, onde x e t são expressos em metros e segundos, respectivamente. Determine (a) quando a velocidade é zero, (b) a posição e