Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 115

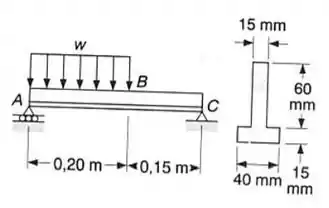
Determinar a carga uniformemente distribuída admissível w para a viga mostrada sabendo se que σadm= 70 MPa na tração σadm= -130 MPa na compressão e que τadm= 60 MPa

Passo 1

Fala aíi gurizada tudo belezinha, espero que simm!!!! Para entendermos melhor a questão vamos fazer um esquema de diagrama de corpo livre? Vejam abaixo!!!

Vamos determinar a distância x:

V A - W x = 0

X = V A W (1)

Agora partiu calcular o momento máximo

+ ↶ ∑ M a = F × d = 0

m   m á x = V A x - W x 2 2 (2)

Substituindo 2 em 1 temos:

m   m á x = V A × V A W - W 2 × ( V A W ) ²

m   m á x = V A 2 2 W (3)

Passo 2

Gurizada a partir do perfil dado no exercicio vamos calcular os momentos na tração e na compressão...

Lembrando que a equação da tensão é dada abaixo, e que a inércia é dada no anexo do livro.

  • Tração

    • σ = m t C i

    70 = m t × 30 787500

    m t = 1,8375   × 10 6   N m m

  • Compressão

σ = m c C i

130 = m t × 45 787500

m c = 2,275   × 10 6   N m m

Para o momento em f calculamos da mesma maneira...

37 , 5 = m f × 30 432000

m f = 0,54 × 10 6   N m m

Passo 3

Agora sim podemos achar a reação VA, fazendo o somatorio em B...

+ ↶ ∑ M b = F × d = 0

M b = 0,35 V A - W × 0,2 × ( 0,1 + 0,1 )

V A = 0,143 W (4)

Substituindo 4 em 3 temos:

m   m á x = V A 2 2 W

1,8375 = ( 0,143 W ) ² 2 W

W = 180   K N m

Resposta

W = 180   K N m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Assumindo que o eixo do Prob. 7.158 é vazado e que o diâmetro interno é metade do diâmetro externo, determinar o menor diâmetro externo permissível para o eixo.
Resolver o Prob. 161, assumindo que toda a potência de 25h p é absorvida pela engrenagem G .
Resolver o Prob. 162, assumindo que 25k W é absorvido em cada engrenagem.
Determinar a carga uniformemente distribuída admissível w , para a viga mostrada, sabendo-se que σ a d m = + 70M P a na tração, σ a d m = - 130M P a , na compressão, e que τ a d m = 60M P a .
Uma barra de aço uniforme de diâmetro d é içada por cabos de um guindaste, amarrados em A e B . Pede-se: (a) determinar a distância a , entre as extremidades da barra e os pontos onde os cabos estão a