Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 1.Problemas - Ex. 16

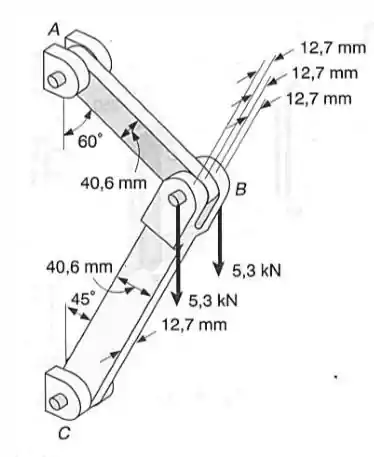
Duas cargas verticais são aplicadas ao pino B da montagem indicada. Sabendo-se que o diâmentro do pino usado em cada ligação é de 15,2   m m , determine o valor máximo da tensão normalmédia na (a) haste AB; (b) haste BC.

Passo 1

Neste exercício o principal é a análise de forças e tensões no pino B , que está submetido a 4 forças: as duas forças de 5,2   k N mencionadas no exercício, a força da haste C B e a força da haste A B .

Então a melhor forma de resolver este problema é fazer o diagrama de corpo livre do pino B para achar as forças das hastes e com as áreas das hastes achar a máxima tensão normal.

Passo 2

Vamos fazero diagrama de corpo livre do pino B e observe que estamos utilizando uma vista letral do conjunto:

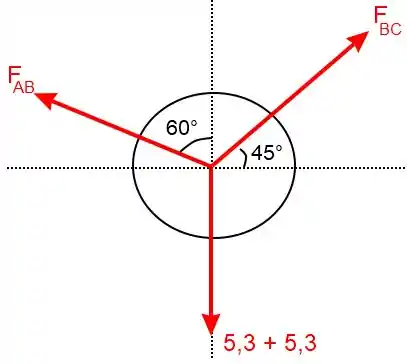
Aqui vai um lembrete: Segundo essa configuração a haste A B estaria sob tensão (porque ela está puxando o pino B ) enquanto a haste B C sob compressão (porque está empurrando o pino B ). Mas existe a possibilidade de termos escolhido os sentidos errados, se isso acontecer vamos achar o resultado negativo e vamos saber que o que era tração vira compressão e vice-versa.

Voltando ao cálculo, agora basta fazer o somatório das forças em x e em y e igualar a zero (porque é um problema estático):

∑ F x = 0

F B C ⋅ cos ⁡ 45 ° - F A B ⋅ sen ⁡ 60 ° = 0

F B C ⋅ 2 2 = F A B ⋅ √ 3 2

F B C = F A B ⋅ 3 √ 2

F B C = F A B ⋅ 6 2

∑ F y = 0

F A B ⋅ cos ⁡ 60 ° + F B C ⋅ s e n 45 ° - 5,3 - 5,3 = 0

F A B ⋅ 1 2 + F A B ⋅ 6 2 ⋅ 2 2 = 10,6

F A B 1 2 + 12 4 = 10,6

F A B 1 2 + 2 3 4 = 10,6

F A B 1 2 + 3 2 = 10,6

F A B ⋅ 1,366 = 10,6

F A B = 10,6 1,366

F A B = 7,76   k N

Substituindo para achar F B C

F B C = F A B ⋅ 6 2

F B C = 7,76 ⋅ 6 2

F B C = 9,5   k N

Passo 3

Agora é só aplicar na equação da tensão normal, considerando a menor área das haste, ou seja, calculando a área da seção transversal menos a área do furo do pino:

A = 40,6 - 15,2 ⋅ 12,7

A = 25,4 ⋅ 12,7

A = 322,58

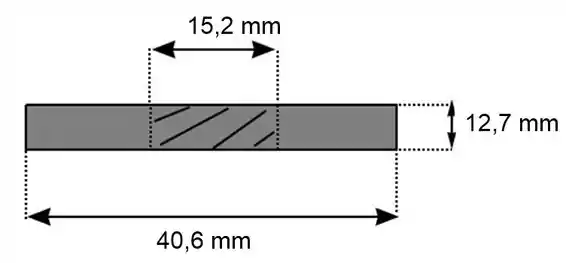
Passo 4

Aplicar a equação para a haste A B

σ = F A

Lembrando que para o resultado estar em M P a devemos utilizar a força em N e a área em m m ²

σ = 7760 322,58

σ = 24   M P a

Esta é uma tensão de tração

Passo 5

Aplicar a equação para a haste B C

σ = F A

σ = 9500 322,58

σ = 29,45   M P a

Esta é uma tensão de compressão.

Resposta

a) Tração

σ = 24   M P a

b) Compressão

σ = 29,45   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determinar a deformação da barra composta do Problema 2.34, se nela atuar uma força centrada de intensidade P = 45 k N .
Uma barra de 250 m m de comprimento, com seção transversal retangular de 15 × 30 m m , consiste de duas lâminas de alumínio ( E = 70 G P a ) , de 5 m m de espessura, e no centro de uma lâmina de latão
Um fio de nylon está sujeito a uma tração de 10N . Sabendo-se que E = 3,45G P a , que a máxima tensão normal admissível é de 40M P a , e que o comprimento do fio não poderá aumentar mais do que 1 % ,
Uma força centrada de 180 k N está aplicada na montagem mostrada, por meio de placas rígidas colocadas em ambas as extremidades. Sabe-se que os módulos de elasticidade do aço e do alumínio valem 200 G
Uma barra de poliestireno consiste de duas porções cilíndricas AB e BC, restringidas em ambas as extremidades, e suporta duas cargas de 27 k N , como indicado. Sabendo-se que E = 3,1 G P a , determina