Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 7
Se m=150kg, h=500mm e a constante de cada uma das molas
é k-2,5kN/m, determinar a variação dos valores da distância d para que o equilíbrio da barra rígida AB seja estável na posição mostrada. Cada uma das molas pode atuar a tração ou compressão
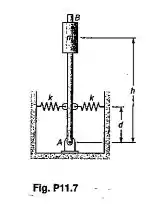
Passo 1
Vamos desenhar o nosso diagrama de corpo livre e tentar imaginar o que acontece com a barra quando são aplicadas as forças P nelas, ok?
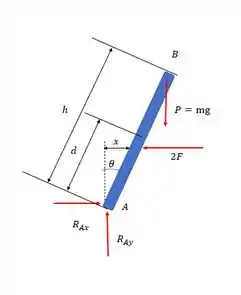
Ao aplicar a força P vai rolar um deslocamento x, e um deslocamento angular e as forças das molas vão reagir em conjunto para parar o deslocamento, no sentido oposto de P. A gente vai buscar um jeito de relacionar o P com as dimensões e a constante da mola, o peso para o qual a coluna está na iminência de girar é o peso crítico e a distância d que levará ao peso crítico é a qual nos interessa.
A força da mola é dada por:
Olhando pra figura a gente pode ver que:
E como os ângulos são bem pequenos nesses casos:
Daí:
Passo 2
Fazendo o somatório dos momentos no ponto A, a gente tem:
Lembrando que se o ângulo é muito pequeno temos:
Substituindo :
Substituindo os valores:
Temos:
Ou seja,d precisa ser: