Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 5.Problemas - Ex. 137
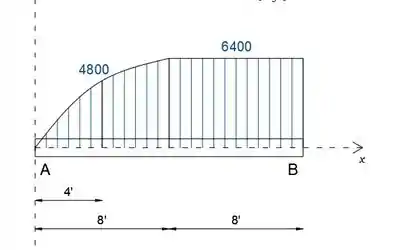
Desenhe os diagramas de cisalhamento e momento para a viga cantilever carregada onde o acoplamento final M_1 é ajustado de modo a produzir o momento zero na extremidade fixa da viga. Encontre o momento fletor M em x = 4 pés
Passo 1
Primeiro, vamos determinar as forças de reação do diagrama de corpo livre usando as equações de equilíbrio. Sabemos que o momento na extremidade fixa é MA = 0, então precisaremos determinar as forças de reação XA, YA e o par M1
Observe que substituímos as cargas distribuídas por suas resultantes
Escreva as equações de equilíbrio:
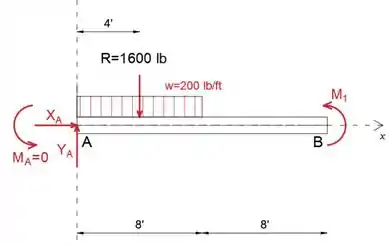
Passo 2
A partir daqui, podemos construir o diagrama de força cortante
Usando a fórmula , calcularemos as forças de cisalhamento da esquerda para a direita
Observe que também vamos calcular a força de cisalhamento em x = 4, pois precisaremos disso para determinar o momento fletor em x = 4
O diagrama da força de cisalhamento tem um salto positivo em A, causado pela força de reação YA, após o qual é linearmente decrescente até atingir zero em x = 8, e é constante até o final B.
Passo 3
A seguir, usaremos o diagrama de força cortante para construir o diagrama de momento fletor
Como sabemos que o momento é igual a zero em x = 0 "" m, e que a mudança no momento é igual à área do diagrama de força cortante, então, usando a expressão , calcularemos os valores do momento fletor nos pontos onde atuam as forças externas.
Observe que a inclinação para o diagrama de momento está diminuindo ao longo do intervalo [0≤x≤8], uma vez que a força cortante diminui ao longo do intervalo [0≤x≤8], enquanto é constante para o resto da viga.
Conforme calculado acima, o momento fletor em x = 4 'é:
