Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 9.Problemas - Ex. 93e

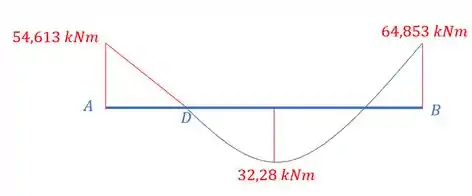
Determinar a reação em A e desenhar o diagrama de momento fletor para a viga com o carregamento mostrado.

Obs: determinação da reação em B e desenho do diagrama de momentos

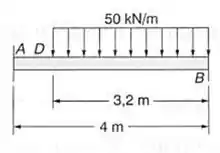
Passo 1

Podemos ir para a última parte que precisamos determinar o diagrama, como já sabemos a reação em A, vamos descobrir a reação em B. assim teremos que:

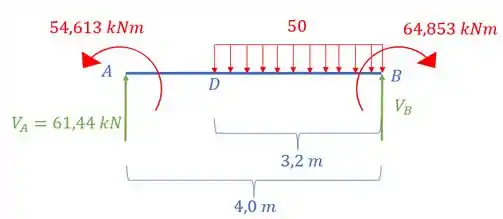
Passo 2

Para determinação do diagrama, precisamos ir ponto por ponto, assim teremos que:

Momento no ponto A e B

Sabe-se que o momento em A e B é concentrado e traciona as fibras da parte de cima, assim, teremos que:

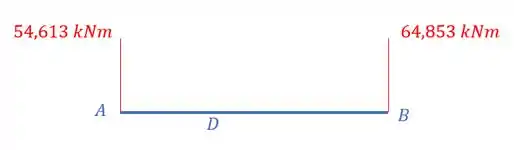
Como temos uma carga distribuída, podemos buscar algum ponto nela em que o cortante seja zero, e assim determinar o ponto em que ocorre o máximo momento, para isso, basta ver em que ponto da carga distribuída a carga do apoio em B zera, assim tem-se que:

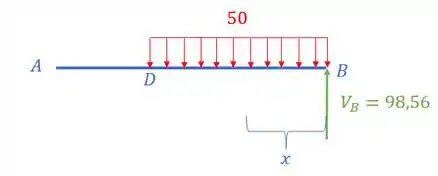
Desse modo, calculando o máximo momento no ponto a do apoio em B, obtém-se que:

assim tem-se que:

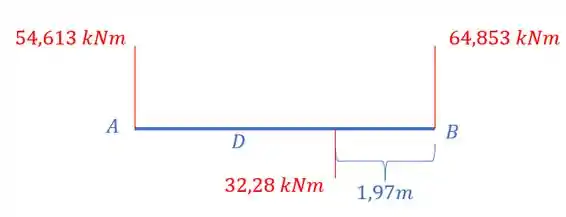
Perceba que entre os trechos A e D não temos carga, ou seja, esse trecho será reto, porém, entre os trechos D e B temos uma carga distribuída, e nesse caso a carga é parabólica com máximo sendo de .

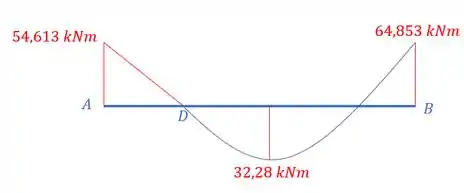
Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a inclinação máxima e a deflexão máxima da viga simplesmente apoiada submetida ao momento M 0 . E I é constante.

Determine as equações da linha elástica utilizando as coordenadas x 1 e x 2 e especifique a inclinação em C e o deslocamento em B . E I é constante.

Uma chave de torque é usada para apertar a porca de um parafuso. Se o mostrador indicar que foi aplicado um torque de 90k N . m quando o parafuso estiver totalmente apertado, determine a força P que a

As partes centrais das duas fitas métricas de madeira estão separadas por um cilindro rígido liso de 50m m de diâmetro. Determine a força F que deve ser aplicada a cada extremidade de modo que suas ex

A viga é feita de um material com peso específico y . Determine o deslocamento e a inclinação em sua extremidade A devido a seu peso. O módulo de elasticidade para o material é E .