Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.5 - Ex. 82
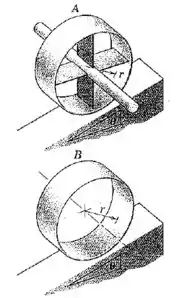
Determine a aceleração angular de cada uma das duas rodas, enquanto rolam sem deslizar para baixo nos planos inclinados. Para a roda , examine o caso em que a massa do aro e dos raios é desprezível e a massa da barra está concentrada ao longo da sua linha de centro. Para a roda , assuma que a espessura do aro é desprezível em comparação com o seu raio, de modo que toda a massa está concentrada no aro. Especifique também o coeficiente de atrito estático mínimo necessário para evitar que cada uma das rodas deslize.
Passo 1
Para o caso da roda , se a massa do aro e dos raios é desprezivel, e o eixo em relação ao qual calculamos o momento de inércia está exatamente sobre a barra, então:
E consequentemente:
Para satisfazer essa condição, a força de atrito deve ser nula, e então:
Ainda pensando nesse caso, podemos aplicar a segunda lei de Newton sobre a direção paralela ao plano:
E a única força agindo nessa direção é uma das componentes da força peso:
E se a roda gira sem deslizar, então , e portanto:
Passo 2
Para o caso , vamos escrever uma equação para o momento resultante em relação ao ponto de contato da roda com o plano.
Nesse caso, o momento gerado pela força de atrito é nulo, e ficamos apenas com o momento da força peso:
O momento de inércia do aro em relação a um eixo que passa pelo ponto é:
Então:
Passo 3
E agora, com esse resultado, podemos escrever a mesma equação em relação ao centro de massa do aro, de forma que a momento do peso seja nulo, e ficamos apenas com o momento da força de atrito .
Com isso poderemos calcular , e consequentemente :
E agora o momento de inércia é :
Agora vamos lembrar da expressão para a força de atrito:
E sabemos que o módulo da força normal é :
Resposta
No primeiro caso temos e . No segundo temos e .