Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Dinâmica Volume 2 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 6.4 - Ex. 37
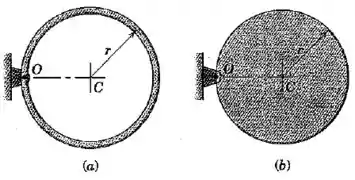
Determine a aceleração angular e a força no mancal em para (a) o anel fino de massa , e (b) o disco circular plano de massa imediatamete apó cada um deles ser liberado a partir do repouso no plano vertical com horizontal.
Passo 1
Vamos fazer a conta forma mais genérica possível, assim podemos aproveitar nosso resultado para os itens (a) e (b).
Imediatamente após o disco ser liberado, a força peso é perpendicular à linha no desenho, e a única outra força que age sobre o disco é a força do mancal em .
Isso quer dizer que se calcularmos o momento total sobre o disco em relação ao ponto , teremos:
E se essa é a aceleração angular do disco, a aceleração linear do centro de massa (que é vertical para baixo nesse instante) é:
E então, aplicando a segunda lei de Newton na direção vertical, e sabendo que as únicas forças agindo nessa direção são o peso e a força do mancal:
Mas como :
Ótimo, chegamos na fórmula geral que queríamos.
Passo 2
Os valores são todos iguais para os itens (a) e (b), com exceção do momento de inércia . Para o anel fino do item (a), o momento de inércia é:
E para o disco circular do item (b) o momento de inércia é:
(a) Então no primeiro caso a força é:
E a acelração angular é:
(b) E no segundo caso:
Resposta
(a) e .
(b) e .