Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 5.Problemas - Ex. 16
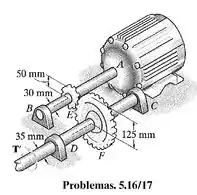
O motor transmite um torque de ao eixo . Esse torque é transmitido ao eixo pelas engrenagens em e . Determine o torque de equilíbrio no eixo e a tensão de cisalhamento máxima em cada eixo. Os mancais , e permitem a livre rotação dos eixos.
Passo 1
Olá!
Um motor impõe um torque no eixo . O torque é transmitido para o eixo usando engrenagens. Os mancais não resistem aos torques.
Vamos anotar tudo que sabemos dos eixos.
Características do eixo :
- Raio do eixo: .
- Momento polar de inércia: .
- Raio da engrenagem em : .
- Raio do eixo: .
- Momento polar de inércia: .
- Raio da engrenagem em : .
Características do eixo :
Na extremidade do eixo , há um torque para equilibrar tudo. Queremos descobrir esse torque!
Então primeiro temos ver como o torque se transmite.
Depois, queremos saber a tensão máxima de cisalhamento em cada eixo. Vamos precisar da fórmula da torção:
E só o que nos falta nessa fórmula são os torques mesmo!
Passo 2
Precisamos descobrir qual é o torque acontecendo em cada eixo. Vamos ver como que torques são transmitidos!
O torque na seção da engrenagem em vai ser o torque imposto pelo motor: . Isso porque não há outro torque ali nem alguma reação.
Podemos dizer que esse torque é gerado por uma força nessa engrenagem distante do seu centro. A fórmulinha do torque fica:
Acontece o mesmo no torque gerado em :
Pelo equilíbrio, como essas engrenagens estão em contato, essas forças precisam ser iguais:
Como não temos outros torques ou reações, esse vai ser o torque do eixo
E como não temos mais nenhum torque agindo (os mancais não reagem nessa questão!), o torque para equilibrar tem que ser
Passo 3
Moleza, já foi a questão quase toda! Agora vamos achar as tensões máximas.
Em , temos torque . Para achar a tensão máxima, é só jogar na fórmula!
E para , temos torque . Então:
Resposta
Torque de equilíbrio: .
Tensão máxima em : .
Tensão máxima em : .