Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 12

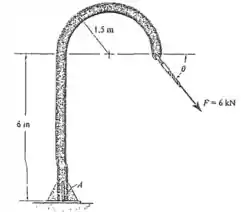
Determine o ângulo θ ( 0 ° ≤ θ ≤ 180 ° ) da força F de modo que ela produza um momento máximo e um momento mínimo em relação ao ponto A . Além disso, quais são as intensidades desses momentos máximo e mínimo?

Passo 1

Oi, galerinha! Tudo bom? Pra começar vamos pensar em alguns conceitos sobre o momento de uma força.

Lembra que o vetor momento é dado por:

M → = F → × d →

Como isso é um produto vetorial, podemos escrever na forma escalar como:

M = F ∙ d ∙ s e n φ

Onde φ é o ângulo entre os vetores força e distância. E visto que o momento depende então da função seno, ela terá o seu valor máximo quando:

φ = 90 °

Nesse caso, o diagrama de corpo livre do exercício vai ser dado por:

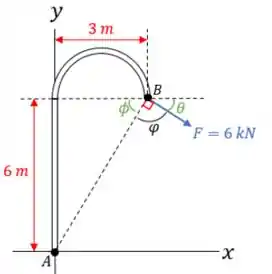
Já para o momento com valor mínimo:

φ = 0 °

Tal que o diagrama é:

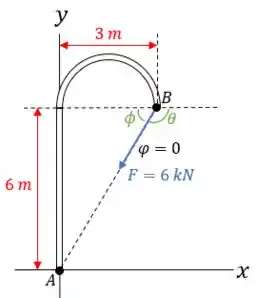
Passo 2

Dessa forma, a partir do primeiro diagrama, podemos definir que o ângulo que dará o momento máximo será definido por:

θ m á x = 180 ° - 90 ° - ϕ = 90 ° - ϕ

Onde, através das relações trigonométricas do triangulo de catetos 3 e 6 formados no diagrama do corpo livre, teremos:

θ m á x = 90 ° - t g - 1 6 3

Logo:

θ m á x = 90 ° - 63,43 °

E, portanto:

θ m á x = 26,57 °

Passo 3

Tendo a angulação máxima, podemos determinar o momento máximo:

M m á x = F ∙ d ∙ s e n φ

Pela temos que:

d = 6 2 + 3 ² = 45

Logo:

M m á x = 6   k N 45 s e n 90 ° = 40,2   k N ∙ m

Passo 4

Da mesma maneira, a partir do desenho ( b ) , podemos definir que o ângulo que dará o momento mínimo será de:

ϕ m í n = t g - 1 6 3 = 63,43 °

Tal que:

θ m í n = 180 ° - ϕ m í n = 180 ° - 63,43 °

θ m í n = 116,57 °

Passo 5

E o momento mínimo terá um valor de:

M m í n = F ∙ d ∙ s e n φ

Logo:

M m í n = F ∙ d ∙ s e n 0 ° = 0

Resposta

θ m á x = 26,57 °

M m á x = 40,2   k N ∙ m

θ m í n = 116,57 °

M m í n = 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Dois garotos empurram o portão como mostrado. Se o garoto em B exerce uma força F B = 150N , determine a intensidade da força F A que o garoto em A precisa exercer para impedir que o portão gire. Desp
As pinças são usadas para prender as extremidades do tubo de perfuração P . Se um torque (momento) M P = 1200N ∙ m é necessário em P para girar o tubo, determine a força que precisa ser aplicada no ca
Determine o momento mínimo produzido pela força F em relação ao ponto A . Especifique o ânguloθ ( 0 ° ≤ θ ≤ 180 ° ) .
A força do tendão de Aquiles F t é mobilizada quando o homem tenta ficar na ponta dos pés. Quando isso é feito, cada um de seus pés fica sujeito a uma força reativa N f = 400N . Se o momento resultant
O membro está sujeito a uma força F = 6k N . Se θ = 45 ° , determine o momento produzido por F em relação ao ponto A .