A força do tendão de Aquiles é mobilizada quando o homem tenta ficar na ponta dos pés. Quando isso é feito, cada um de seus pés fica sujeito a uma força reativa . Se o momento resultante produzido pelas forças e em relação à articulação do tornozelo precisa ser igual a zero, determine a intensidade de .
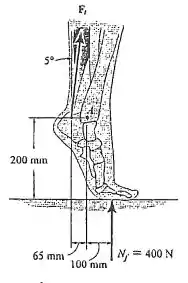
Passo 1
Fala!
Para determinar o valor da força é necessário determinar as distâncias do ponto até as linhas de atuação das forças onde os momentos serão aplicados e, então, utilizar o princípio dos momentos, a fim de isolar a variável a ser determinada na equação.
Vamos olhar para .
Imagina a linha de atuação dessa força. Ela é paralela ao eixo vertical. A distância entre essa linha e o ponto A é:
Agora vamos olhar . Percebe que essa é uma força inclinada. Então é bom que a gente decomponha em relação aos eixos vertical e horizontal.

Percebe que a linha de ação da componente horizontal passa por , logo essa força não gera momento em . Mas a outra componente gera e a distância entre sua linha de atuação e é
Passo 2
O momento causado por vai estar no sentido anti-horário e vai valer:
E o de vai estar no setido horário e vai valer
Como ele disse que o momento em vale zero:
Dessa forma, considerando que os momentos positivos agem no sentido anti-horário, tem-se que: