Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 5
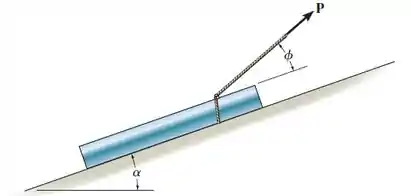
O tubo com peso deve ser puxado para cima no plano indicado com inclinação usando uma força . Se age em um ângulo , mostre que, para deslizar, , onde é o ângulo de atrito estático; .
Passo 1
E aí Pessoal, tudo bem? Vamos dar início a mais uma questão juntos!
Precisamos mostrar que a relação para a força que faz com que o corpo deslize é . Esta força será dada quando a barra está na iminência do movimento. Isto é, quando a força equilibra a força de atrito.
Portanto, a chave para esta questão é o diagrama de corpo livre do nosso corpo. Então, vejamos ele abaixo:
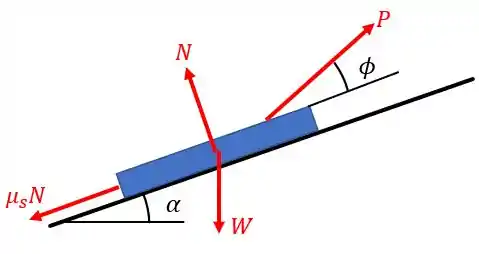
OBS: Não se esqueçam da força peso para baixo!
Agora que já sabemos o que fazer, vamos aos cálculos!
Passo 2
Agora vamos utilizar as equações de equilíbrio. Vamos avaliar o somatório de forças em ambas as direções horizontais e verticais (de acordo com o plano inclinado, como mostramos no diagrama de corpo livre feito no Passo 1).
Então, temos:
Da segunda equação nós obtemos que . Já do enunciado da questão nós temos que . Logo, temos .
Então, se a gente faz essas substituições na equação do , temos:
Passo 3
Para finalizarmos a questão, temos que dar o pulo do gato.
Vamos reescrever como e reorganizar a nossa função. Vejamos só:
Agora é só utilizarmos as relações trigonométricas de soma de arcos. Portanto,
E assim finalizamos a questão!