Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 2.Problemas - Ex. 15
2.15. Determine o ângulo entre os tirante AB e AC, de modo que a força horizontal de tenha uma componente de que atue para a esquerda, na direção de B para A. Considere .
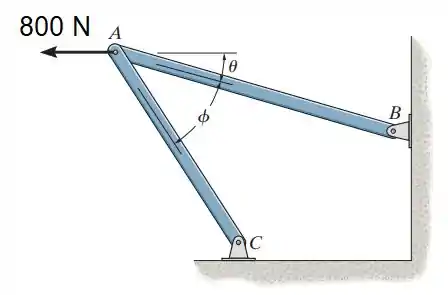
Passo 1
Vamos analisar os vetores, estendendo-os para formar um paralelogramo
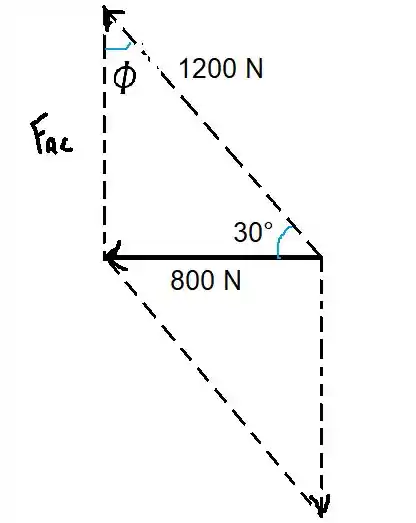
Daqui podemos extrais o seguinte triângulo
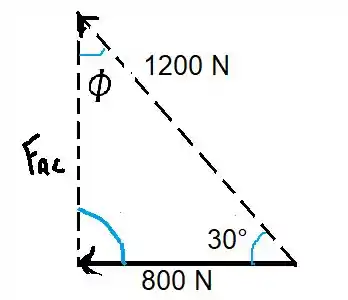
Passo 2
Para descobrir podemos usar a lei dos cossenos
Passo 3
A gente descobriu para podermos saber tudo que precisamos sobre o nosso triângulo para poder calcular , e faremos isso através da lei dos senos
Resposta
Exercícios de Livros Relacionados
Demonstre que ∫ r ˙ r - r r ˙ r 2 d t = r r + C onde C é um vetor constante.
Demonstre que: a )∑ i , j ε i j k δ i j = 0 b )∑ j , k ε i j k ε l j k = 2 δ i l c )∑ i j k ε i j k ε i j k = 6
Utilize a notação ε i j k e derive a identidade A × B × C × D = A B D C - A B C D
Encontre o ângulo entre as superfícies definidas por r 2 = 9ex + y + z 2 = 1n op o n t o2 ,- 2 ,1 .
Determine o valor da integral ∫ S A ∙ d a , onde A = (x2 + y2 + z2)(xi + yj + zk) e a superfície S é definida pela esfera R2 = x2 + y2 + z2. Calcule a integral diretamente e também utilizando o teorem