Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 35

Determine os ângulos θ para haver equilíbrio do cilindro de 100 kg e investigue a estabilidade em cada posição. A mola tem uma rigidez de k = 6 k N m e um comprimento livre de 225 mm

Passo 1

Desenhando o diagrama do corpo livre do corpo:

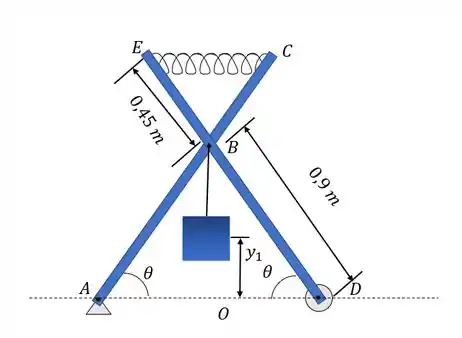
Passo 2

Da geometria do problema:

B O = 0,9 ⋅ sen ⁡ θ k + y 1 = 0,9 ⋅ s e n θ y 1 = 0,9 s e n θ - k k é o comprimento da corda

E C = 2 ⋅ 0,45 c o s θ = 0,9 c o s θ

Passo 3

O próximo passo é calcular a elongação da mola:

s = s - s 0 s = E C - l 0 = 0,9 c o s θ - 0,225

Passo 4

Calculando a função da energia potencial:Energia potencial do cilindro: V g = m ⋅ g ⋅ y 1 = W y 1 = 100 × 9,81 ( 0,9 s e n θ - k )

Energia potencial da mola:   V s = 1 2 k ⋅ s 2 = 1 2 × 6000 × 0,9 c o s θ - 0,225 2

Portanto, a expressão final total da energia potencial é:

V = V g + V s = 100 × 9,81 0,9 s e n θ - k + 1 2 × 6000 × 0,9 c o s θ - 0,225 2 V = V g + V s = 100 × 9,81 0,9 s e n θ - k + 1 2 × 6000 × 0,81 cos 2 ⁡ θ - 0,405 c o s θ +   0,0506 2 V = 882,9 ⋅ s e n θ - 981   k + 2430 cos 2 ⁡ θ + 152 - 1215 c o s θ

Passo 5

Para achar a posição de equilíbrio, precisamos calcular a primeira derivada da expressão:

d V d θ = 882,9 c o s θ - 4860 c o s θ ⋅ s e n θ + 1215 s e n θ d V d θ = 0 ⇒ 882,9 c o s θ - 4860 c o s θ ⋅ s e n θ + 1215 s e n θ

Essa expressão pode ser resolvida por tentativa e erro já que não existe uma formula analítica de se obter a solução. Usando um software computacional: θ = 14,2 º θ = 72 º

Passo 6

Para analisar a estabilidade, devemos calcular a expressão da segunda derivada: d 2 V d θ 2 = - 882,9 s e n θ - 4860 - s e n θ ⋅ s e n θ + c o s θ c o s θ + 1215 cos ⁡ θ d 2 V d θ 2 θ = 14,2 º = - 882,9 s e n 14,2 º - 4860 - s e n 14,2 º ⋅ s e n 14,2 º + c o s 14,2 º c o s 14,2 º + 1215 cos ⁡ 14,2 º d 2 V d θ 2 θ = 14,2 º = - 3314 > 0 = > i n s t á v e l

d 2 V d θ 2 θ = 72 º = - 882 s e n 72 º - 4860 - s e n 72 º ⋅ s e n 72 º + c o s 72 º c o s 72 º + 1215 cos ⁡ 72 º d 2 V d θ 2 θ = 72 º = 3468 > 0   ( e s t á v e l )

Resposta

θ = 14,2 º   e q u i l í b r i o   i n s t á v e l θ = 72 º     e q u i l i b r i o   e s t á v e l

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A mola AB, de constante k , está indeformada quando θ = 0 , determine (a) os intervalos de θ para equilíbrio estável e (b) dois valores para equilíbrio tal que P é metade do limite superior encontrado
Se a mola está indeformada quando seu comprimento vale o raio r , determine o valor do ângulo para equilíbrio se W = 225 N ,r = 225 m m ek = 2,7 k N / m .
A haste AB está presa a uma articulação em A e a duas molas, cada qual de constante k. Se h = 625 mm, d -=300 mm e W = 360 N, determine o intervalo de valores dc k para os quais o equilíbrio da haste
Se uma carga W de 450N é aplicada ao mecanismo em C, sabendo que a mola está indeformada quando θ = 30 , determine o valor de θ para equilíbrio e determine a estabilidade.
A barra vertical AD é fixada por duas molas de constante k e está em equilíbrio na posição mostrada. Determine o intervalo de valores da intensidade P para duas forças verticais iguais e opostas Pe —