Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 11.Problemas - Ex. 42
A xícara tem um fundo hemisférico e uma massa m. Determine a posição h do centro de massa G de modo que a xícara esteja em equilíbrio indiferente.
Passo 1
Desenhando o diagrama do corpo livre:
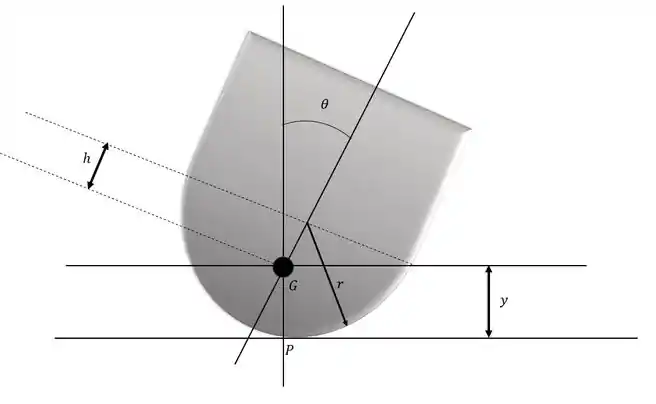
Passo 2
Da geometria da figura:
Passo 3
Calculando a energia potencial da xícara:
Passo 4
Para encontrar a posição de equilíbrio, devemos encontrar a primeira derivada da função potencial:
Passo 5
Para analisar a estabilidade, precisamos calcular a segunda derivada da função potencial:
Para que a xícara esteja em equilíbrio indiferente, :
Resposta
A altura que proporciona equilíbrio indiferente para a xícara ocorre em
Exercícios de Livros Relacionados
Se cada um dos três elementos do mecanismo tem peso W , determine o ângulo θ de equilíbrio. A mola, que sempre permanece na vertical, não está deformada quando θ = 0 ° .
Uma mola com rigidez à torção k está presa à articulação em B . Ela não está deformada quandoo conjunto de hastes está na posição vertical. Determine o peso W do bloco que resulta em equilíbrio neutro
Se a haste uniforme O A tem massa de 12k g , determine a massa m que a manterá em equilibrio quando θ = 30 ∘ . O ponto C coincide c o m B quando OA está na horizontal. Despreze o tamanho da polia em
Se a mola tem rigidez à torsão k = 300N ⋅ m / r a d e não está deformada quando θ = 90 ∘ , determine o ângulo de equilibrio se a esfera tem massa de 20k g . Investigue a estabilidade nessa posição. A
O cilindro está apoiado em A , vértice de um furo cônico em sua base. Determine a distância míni m a d a fim de que ele permaneça em equilibrio estável.